- Ecuaciones de figuras geométricas
-
Anexo:Ecuaciones de figuras geométricas
Ecuaciones de las figuras geométricas más usuales.
Figuras de dos dimensiones
Polígonos
Nombre Área interior Perímetro Aristas Vértices Comentarios Triángulo 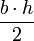
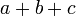
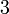
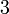
b es el tamaño de la base, h la altura, a y c el tamaño de los otros dos lados Triángulo equilátero 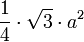
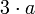
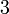
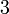
a es el tamaño de un lado Cuadrado 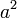
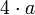
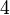
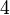
a es el tamaño de un lado Rombo 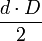
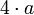
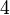
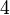
a es el tamaño de un lado, d la diagonal menor, y D la diagonal mayor Rectángulo 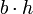
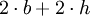
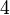
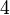
b es el tamaño de la base, h es la altura Paralelogramo 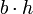
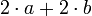
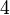
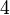
b es el tamaño de la base, a es el tamaño del lado no paralelo al anterior, h es la altura Trapecio 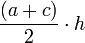
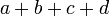
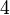
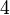
a es el tamaño de un lado paralelo, c es el tamaño del otro lado paralelo, h es la altura, b y d los otros lados Pentágono regular 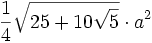
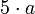
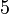
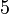
a es el tamaño de un lado Polígono regular 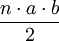
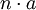
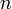
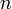
a es el tamaño de un lado, b es la apotema del polígono, y n el número de lados Polígono regular 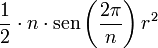
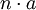
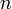
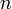
a es el tamaño de un lado, r es la distancia desde el centro a un vértice, n es el número de lados del polígono Figuras curvas
Nombre Área Longitud Comentarios Circunferencia no tiene 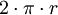
donde  es el tamaño del radio
es el tamaño del radioCírculo 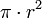
donde  es el tamaño del radio
es el tamaño del radioElipse 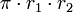
Área interior: 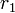 es el tamaño de un semieje, y
es el tamaño de un semieje, y 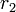 el tamaño del otro
el tamaño del otroFiguras de tres dimensiones
Poliedros
Nombre Volumen Superficie Caras Aristas Vértices Comentarios Cubo 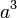
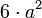
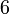
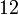
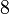
a es el tamaño de la arista Tetraedro 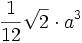
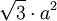
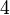
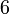
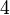
a es el tamaño de la arista Figuras curvas
Nombre Volumen Superficie Comentarios Cilindro 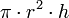
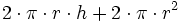
r es el tamaño del radio, h es la altura Cono 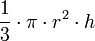
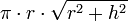
r es el tamaño del radio, h es la altura Esfera 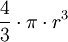
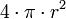
r es el tamaño del radio Esferoide 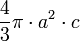
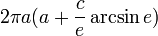
siendo a y c los semiejes, estando situado c en el eje de coordenadas z, siendo e la excentricidad de la elipse. Elipsoide 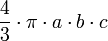
siendo a, b y c los semiejes del elipsoide. Toro 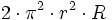
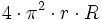
r es el tamaño del radio interior (circunferencia rotada), y R el tamaño del radio de revolución. Toroide 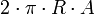
A es el área interior de la figura generatriz, y R es la longitud del radio de revolución (desde el eje al centro de simetría de la figura generatriz). Figuras de cuatro dimensiones
Politopos
Nombre Hiper-volumen Hiper-área Poliedros Caras Aristas Vértices Comentarios Hipercubo 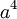
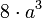
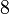
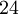
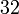
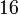
a es el tamaño de la arista Pentácoro 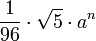
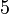
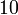
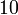
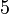
a es el tamaño de la arista Figuras curvas
Nombre Hiper-volumen Hiper-área Comentarios Hiperesfera 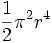
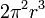
r es el tamaño del radio Figuras de n dimensiones
Familia Espacio (n) Espacio (n-1) Comentarios Cuadrado, cubo, hipercubo... 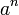
a es el tamaño de una arista, n es la dimensión Triángulo equilátero, tetraedro, pentácoro... 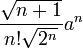
a es el tamaño de una arista, n es la dimensión Círculo, esfera, hiperesfera... 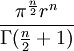
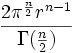
r es el tamaño del radio, n es la dimensión Categorías: Figuras geométricas | Anexos:Matemáticas
Wikimedia foundation. 2010.
