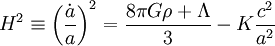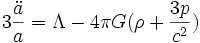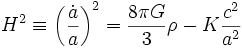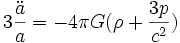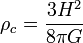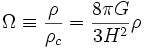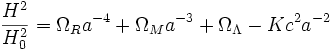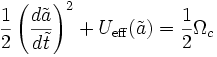- Ecuaciones de Friedmann
-
Ecuaciones de Friedmann
Las ecuaciones de Friedmann son un conjunto de ecuaciones utilizadas en cosmología física que describen la expansión métrica del espacio en modelos homogéneos e isótropos del Universo dentro del contexto de la Teoría General de la Relatividad. Fueron halladas por Alexander Friedman en 1922[1] a partir de las ecuaciones de campo de Einstein para la métrica de Friedman-Lemaître-Robertson-Walker y un fluido con una densidad de energía (ρ) y una presión (p) dadas. Las ecuaciones son:
donde Λ es la constante cosmológica, posiblemente causada por la energía del vacío, G es la constante de gravitación, c es la velocidad de la luz, a es el factor de escala del Universo y K es la curvatura gaussiana cuando a = 1 (p.ej. hoy). Si la forma del universo es hiperesférica y R es el radio de curvatura (R0 en el momento actual), entonces a = R / R0. Generalmente,
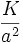 es la curvatura gaussiana. Si K es positiva, entonces el Universo es hiperesférico. Si K es cero, el Universo es plano, y si K es negativo, el Universo es hiperbólico. Nótese que ρ y p son función de a. El parámetro de Hubble, H, es la velocidad de expansión del universo.
es la curvatura gaussiana. Si K es positiva, entonces el Universo es hiperesférico. Si K es cero, el Universo es plano, y si K es negativo, el Universo es hiperbólico. Nótese que ρ y p son función de a. El parámetro de Hubble, H, es la velocidad de expansión del universo.Estas ecuaciones a veces se simplifican redefiniendo la densidad de energía y la presión:
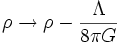
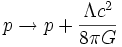
para obtener:
El parámetro de Hubble puede cambiar en el tiempo si otros miembros de la ecuación son dependientes del tiempo (en particular la densidad de energía, la energía del vacío y la curvatura). Evaluando el parámetro de Hubble en el momento actual produce que la constante de Hubble que es la constante de proporcionalidad de la ley de Hubble. Aplicado a un fluido con una ecuación de estado dada, las ecuaciones de Friedmann dan como resultado la evolución en el tiempo y la geometría del Universo como función de la densidad del fluido.
Algunos cosmólogos llaman a la segunda de estas dos ecuaciones la ecuación de aceleración y se reservan el término ecuación de Friedmann sólo para la primera ecuación.
El parámetro de densidad
El parámetro de densidad, Ω, se define como la relación de la densidad actual (u observada) ρ respecto a la densidad crítica ρc del Universo de Friedmann. Una expresión para la densidad crítica se encuentra asimiendo que Λ es cero (como es para todos los Universos de Friedmann básicos) y estableciendo la curvatura K igual a cero. Cuando se sustituyen estos parámetros en la primera ecuación de Friedmann se encuentra que:
y se obtiene que la expresión para el parámetro de densidad (útil para comparar diferentes modelos cosmológicos) es:
Este término originalmente fue utilizado como una manera de determinar la geometría del campo en el que ρc es la densidad crítica para la que la geometría es plana. Asumiendo una densidad de energía del vacío nula, si Ω es mayor que uno, la geometría es cerrada y el Universo eventualmente parará su expansión y entonces se colapsará. Si Ω es menor que uno, será abierto y el Universo se expandirá para siempre. Sin embargo, también se pueden sintetizar los términos de curvatura y de la energía del vacío en una expresión más general para Ω en el caso de que este parámetro de densidad de energía sea exactemente igual a la unidad. Entonces es una cuestión de medir los diferentes componentes, normalmente designados por subíndices. De acuerdo con el modelo Lambda-CDM, hay importantes componentes de Ω debido a bariones, materia oscura fría y energía oscura. La geometría del espacio-tiempo fue medida por el satélite WMAP estando cerca de ser una geometría plana, es decir, el parámetro de curvatura K es aproximadamente cero.
La primera Ecuación de Friedmann a menudo se escribe formalmente con los parámeros de densidad.
Donde, ΩR es la densidad de radiación actual, ΩM es la densidad de materia (oscura más la bariónica) actual y ΩΛ es la constante cosmológica o la densidad de vacío actual.
Ecuación de Friedmann reescalada
Estableciendo
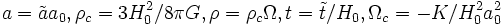 donde a0 y H0 son por separado el factor de escala y el parámetro de Hubble actuales. Entonces podemos hallar que:
donde a0 y H0 son por separado el factor de escala y el parámetro de Hubble actuales. Entonces podemos hallar que:donde
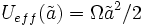 . Para cualquier forma del potencial efectivo
. Para cualquier forma del potencial efectivo 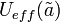 , hay una ecuación de estado p = p(ρ) que la producirá.
, hay una ecuación de estado p = p(ρ) que la producirá.Referencias
- ↑ Friedmann, A: Über die Krümmung des Raumes, Z. Phys. 10 (1922), 377-386. (Traducción al inglés en ¡: Gen. Rel. Grav. 31 (1999), 1991-2000.)
Categorías: Cosmología física | Relatividad general | Ecuaciones
Wikimedia foundation. 2010.