- Conjetura de Goldbach
-
En teoría de números, la conjetura de Goldbach es uno de los problemas abiertos más antiguos en matemáticas. A veces se le califica del problema más difícil en la historia de esta ciencia. Su enunciado es el siguiente:
Todo número par mayor que 2 puede escribirse como suma de dos números primos.
Christian Goldbach (1742)Cabe notar que se puede emplear dos veces el mismo número primo.
Por ejemplo,
Historia
Esta conjetura había sido conocida por Descartes. La siguiente afirmación es equivalente a la anterior y es la que se conjeturó originalmente en una carta de Goldbach a Euler en 1742:
- Todo número entero mayor que 5 se puede escribir como suma de tres números primos.
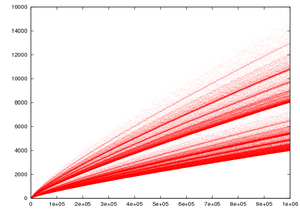
Esta conjetura ha sido investigada por muchos teóricos de números y ha sido comprobada por ordenadores para todos los números pares menores que 1018. La mayor parte de los matemáticos cree que la conjetura es cierta, y se basan mayoritariamente en las consideraciones estadísticas sobre la distribución probabilística de los números primos en el conjunto de los números naturales: cuanto mayor sea el número entero par, se hace más "probable" que pueda ser escrito como suma de dos números primos.
Sabemos que todo número par puede escribirse de forma mínima como suma de a lo más seis números primos. Como consecuencia de un trabajo de Vinográdov, todo número par lo bastante grande puede escribirse como suma de a lo más cuatro números primos. Además, Vinográdov demostró que casi todos los números pares pueden escribirse como suma de dos números primos (en el sentido de que la proporción de números pares que pueden escribirse de dicha forma tiende a 1). En 1966, Chen Jing-run mostró que todo número par lo bastante grande puede escribirse como suma de un primo y un número que tiene a lo más dos factores primos.
Con el fin de generar publicidad para el libro El tío Petros y la conjetura de Goldbach de Apostolos Doxiadis, el editor británico Tony Faber ofreció en 2000 un premio de un millón de dólares a aquel angloparlante que demostrase la conjetura antes de abril de 2002. Nadie reclamó el premio.
Goldbach formuló dos conjeturas relacionadas entre sí sobre la suma de números primos: la conjetura 'fuerte' de Goldbach y la conjetura 'débil' de Goldbach. La que se discute aquí es la fuerte, y la que se suele mencionar como "conjetura de Goldbach" a secas.
Obras influenciadas por esta Conjetura
En cine:
- La conjetura de Goldbach forma parte de la trama de la película española La habitación de Fermat (2007).
- También aparece en la película Proof, conocida en España como La verdad oculta (2005).
- En la segunda película de Futurama, La bestia con un millón de espaldas (2008), el profesor Hubert Fansworth la menciona.
En literatura:
- El tío Petros y la Conjetura de Goldbach es una novela de Apostolos Doxiadis que gira en torno a la vida de un joven cuyo tío dedicó su vida a intentar resolver esta conjetura.
- Ubu Rey es una obra teatral de Alfred Jarry que instaura una extraña relación de esta conjetura al ironizar al poder político como resultado de la suma y unión unidades afines de poder.
Enlaces externos
- Carta original escrita por Christian Golbach para Euler (en alemán)
- Mathworld http://mathworld.wolfram.com/GoldbachConjecture.html
- Chris Caldwell: Goldbach's conjecture, parte de las Prime Pages (Páginas sobre números primos): http://www.utm.edu/research/primes/glossary/GoldbachConjecture.html
- Anjana Ahuja: A million-dollar maths question (Una pregunta de matemáticas de un millón de dólares), The Times, March 16, 2000: http://www.times-archive.co.uk/news/pages/tim/2000/03/16/timfeafea02004.html
Categorías:- Teoría aditiva de números
- Teoría analítica de números
- Conjeturas matemáticas
- Problemas no resueltos de la matemática
Wikimedia foundation. 2010.