- Rango de una matriz
-
Rango de una matriz
En álgebra lineal, el rango de una matriz es el número de columnas (filas respectivamente) que son linealmente independientes. Si el rango fila y el columna son iguales, este número es llamado simplemente rango de A. Comúnmente se expresa como R(A).
El número de columnas independientes de una matriz m por n A es igual a la dimensión del espacio columna de A. También la dimensión del espacio fila determina el rango. El rango de A será, por tanto, mayor o igual que uno y menor o igual que el mínimo entre m y n.
Contenido
Rango de una transformación lineal
El rango es una propiedad no sólo de las matrices sino extendible a las aplicaciones lineales de las cuales las matrices son una representación fijada la base. Definamos en primer lugar el concepto de rango de una aplicación lineal de forma genérica. Dada aplicación o transformación lineal:
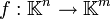
Se define el rango simplemente como la dimensión del conjunto imagen de la aplicación:
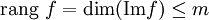
Una propiedad muy importante del rango así definido y el rango de matrices definido anteriormente, es que ambos coinciden. Es decir, dada una base arbitraria la aplicación lineal se puede representar mediante esa base en forma de matriz resultando el rango de esa matriz idéntico al rango de la apliación lineal que representa.
Para establecer más claramente la relación entre el rango de una aplicación lineal y una matriz que represente dicha aplicación lineal, deben fijarse dos bases vectoriales en cada uno de los dos espacios
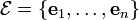 y
y 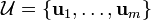 podemos expresar la transformación lineal por una matriz
podemos expresar la transformación lineal por una matriz ![A_\mathcal{E,U} = [a_{ij}]](/pictures/eswiki/102/fe2f089faeab85e9872c1f84a59f7631.png) como una en una cierta base:
como una en una cierta base: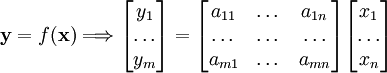
Siendo:
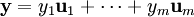 , la imagen del vector x.
, la imagen del vector x.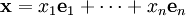 , la antiimagen del vector y.
, la antiimagen del vector y.
Como se dija anteriormente, puede demostrarse que el rango de
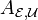 coincide con la dimensión de la imagen de f (véase transformación lineal para más detalles acerca de la imagen y el kernel).
coincide con la dimensión de la imagen de f (véase transformación lineal para más detalles acerca de la imagen y el kernel).Ejercicios de Rango de Matrices
Cálculo del rango
Dada una aplicación lineal su rango puede calcularse fácilmente considerando una base cualquiera y determinando el rango de la matriz que representa la aplicación en dicha base, ya que el número obtenido no dependerá de la elección de la base.
Dada una matriz su rango puede determinarse sencillamente a partir del cálculo de determinantes. Dada la matriz
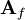 de una aplicación lineal
de una aplicación lineal 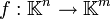 :
:
se define el rango como el máximo entero r tal que existe un menor no nulo de orden r:
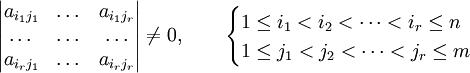
Otra forma de obtener el rango de una matriz es mediante el método de Gauss-Jordan, y será igual al número de filas no nulas de la matriz obtenida con este método.
Aplicaciones
Una útil aplicación de calcular el rango de una matriz es la de determinar el número de soluciones al sistema de ecuaciones lineales. El sistema tiene por lo menos una solución si el rango de la matriz de coeficientes equivale al rango de la matriz aumentada. En ese caso, ésta tiene exactamente una solución si el rango equivale al número de incógnitas; en otro caso, la solución general tiene k parámetros libres, donde k es la diferencia entre el número de incógnitas y el rango.
Una matriz es invertible (tiene inversa) si y sólo si su rango es máximo.
En teoría de control, el rango de una matriz se puede usar para determinar si un sistema lineal es controlable u observable.
Categorías: Matrices | Álgebra lineal
Wikimedia foundation. 2010.
