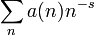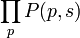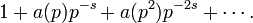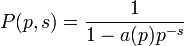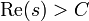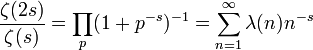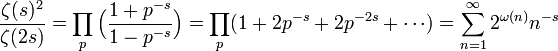Producto de Euler

Producto de Euler

Saltar a navegación, búsqueda

Leonhard Euler.

En matemática, un producto de Euler es la expansión de un producto infinito, indexado por números primos p de una serie de Dirichlet. El nombre surge del caso especial de la función zeta de Riemann, cuya representación en forma de producto, fue probada por Leonhard Euler en 1737.

Definición

En general, una serie de Dirichlet de la forma

$\sum_{n} a(n)n^{-s}\,$

donde a(n) es una función multiplicativa de n, puede ser escrita de la forma

$\prod_{p} P(p,s)\,$

donde P(p,s) es la suma

$1+a(p)p^{-s} + a(p^2)p^{-2s} + \cdots .$

En efecto, si consideramos éstas como funciones generadoras de manera formal, la condición necesaria y suficiente para la existencia del producto de Euler equivalente a la serie es que a(n) sea multiplicativa, o sea, que a(n) sea igual al producto de a(p^k) para los distintos factores primos p que componen n.

Un caso importante es cuando a(n) es una función totalmente multiplicativa, donde se cumple que P(p,s) es una serie geométrica. Entonces

$P(p,s)=\frac{1}{1-a(p)p^{-s}}$

como puede ser el caso de la función zeta de Riemann, donde a(n) = 1, y más generalmente, para los caracteres de Dirichlet.

En la práctica, todos los casos importantes a tener en cuenta son las series y productos infinitos que son absolutamente convergentes en cierta región

$\operatorname{Re}(s) > C$

o sea, en la parte derecha del semiplano formado por números complejos. Esto da también alguna información, dado que el producto infinito, al converger, debe dar una valor distinto de cero, y también que la función dada por la serie infinita no es cero en dicho semiplano.

Ejemplos de productos de Euler

• El producto de Euler correpondiente a la función zeta de Riemann, usando también la suma de series geométricas es:

$\zeta(s) = \sum_{n=1}^{\infty}n^{-s} = \prod_{p} \Big(\sum_{n=0}^{\infty}p^{-ns}\Big) = \prod_{p} (1-p^{-s})^{-1}$.

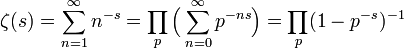• El producto de Euler de la función de Möbius μ(n) es:

$\frac{1}{\zeta(s) }= \prod_{p} (1-p^{-s})= \sum_{n=1}^{\infty}\mu (n)n^{-s}$.

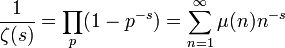• Productos más específicos derivados de la función zeta son:

$\frac{\zeta(2s)}{\zeta(s) }= \prod_{p} (1+p^{-s})^{-1} = \sum_{n=1}^{\infty}\lambda (n)n^{-s}$

donde λ(n) = ( − 1)^Ω(n) es la función de Liouville, y

$\frac{\zeta(s)}{\zeta(2s) }= \prod_{p} (1+p^{-s}) = \sum_{n=1}^{\infty} |\mu(n)|n^{-s}$.

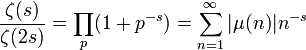• De manera similar

$\frac{\zeta(s)^2}{\zeta(2s)} = \prod_{p} \Big(\frac{1+p^{-s}}{1-p^{-s}}\Big) = \prod_{p} (1+2p^{-s}+2p^{-2s}+\cdots) = \sum_{n=1}^{\infty}2^{\omega(n)} n^{-s}$

donde ω(n) cuenta el número de divisores primos distintos de n y 2^ω(n) el número de divisores de la forma cuadrado libre.

Si χ(n) es el carácter de Dirichlet del conductor N, tal que si χ es totalmente multiplicativa y χ(n) sólo depende de n modulo N, y χ(n) = 0 si n no es coprimo con N, entonces:

$\prod_{p} (1- \chi(p) p^{-s})^{-1} = \sum_{n=1}^{\infty}\chi(n)n^{-s}$.

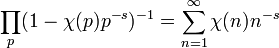Aquí es conveniente omitir los número primos p que dividen al conductor N del producto.

Ramanujan, es sus cuadernos, trató de generalizar el producto de Euler para la función zeta en la forma:

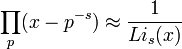$\prod_{p} (x-p^{-s})\approx \frac{1}{Li_{s} (x)}$ s > 1

(donde Li_s (x) es la función polilogaritmo)

buscando la forma de obtener potencias primas como raíces de cierta función f(x, s).

Véase también

• Función zeta de Riemann
• Función L de Dirichlet
• Producto de Euler para la función zeta de Riemann

Referencias

• Euler, Leonhard, Variae observations circa series infinitas, Commentarii academiae scientiarum Petropolitanae 9 (1737), 1744, p. 160-188. Reprinted in Opera Omnia Series I volume 14, p. 216-244.
• G. Polya, Induction and Analogy in Mathematics Volume 1 (1954) Princeton University Press L.C. Card 53-6388
• Tom M. Apostol, Introduction to Analytic Number Theory, (1976) Springer-Verlag, New York. ISBN 0-387-90163-9
• G.H. Hardy and E.M. Wright, An introduction to the theory of numbers, 5th ed., Oxford (1979) ISBN 0-19-853171-0

Enlaces externos

• http://www.EulerArchive.org (en inglés)
• Euler, Leonhard, Variae observations circa series infinitas, Commentarii academiae scientiarum Petropolitanae 9 (1737), 1744, p. 160-188 (Traducido al inglés) [1]
• Ramanujan lost notebook [2]
• planetmath.org (2008). «Euler product.». Consultado el 15 de julio de 2008.
• Wolffram.Mathworld.com (2008). «Euler product.». Consultado el 15 de julio de 2008.

Obtenido de "Producto de Euler"