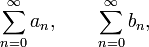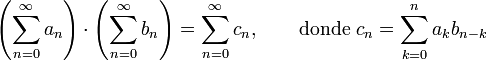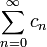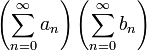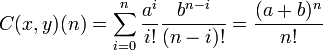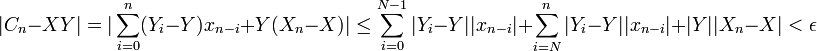- Producto de Cauchy
-
Producto de Cauchy
En matemáticas, el producto de Cauchy, (en honor a Augustin Louis Cauchy), de dos series estrictamente formales (aunque no necesariamente convergentes)
por lo general, de números reales o complejos, se define mediante una convolución discreta. Siendo el producto de Cauchy:para n = 0, 1, 2,...
"Formal" significa que las series se manipulan sin prestar atención a aspectos de convergencia. No es preciso que las series sean convergentes. Véase por ejemplo series de potencia formales.Es de esperar, que por analogía con las sumas finitas, en el caso en que las dos series fueran convergentes, la suma de la serie infinita
sea igual al producto
de la misma manera en que esto sería correcto cuando cada una de las dos sumas que se multiplican posee un número finito de términos.En casos suficientemente bien comportados, se cumple con la expresión anterior. Pero—y este es un punto importante—el producto de Cauchy de dos sucesiones existe aún en el caso que una o ambas de las series infinitas correspondientes no fueran convergentes.
Contenido
Ejemplos
Serie finita
xi = 0 para todo i > n y yi = 0 para todo i > m. En este caso el producto de Cauchy de
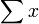 y
y 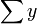 se verifica es
se verifica es 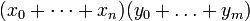 . Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.
. Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.Serie infinita
- Primer ejemplo. Para alguna
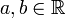 , sea
, sea 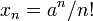 y
y 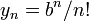 . Entonces
. Entonces
por definición y la fórmula binomial. Dado que, formalmente,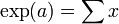 y
y 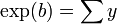 , se ha demostrado que
, se ha demostrado que 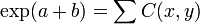 . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series (véase debajo), se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo
. Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series (véase debajo), se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo 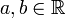 .
.- Segundo ejemplo. Sea x(n) = 1 para todo
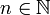 . Entonces C(x,x)(n) = n + 1 para todo
. Entonces C(x,x)(n) = n + 1 para todo 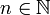 por lo tanto el producto de Cauchy
por lo tanto el producto de Cauchy 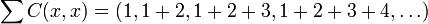 y no es convergente.
y no es convergente.
Convergencia y teorema de Mertens
Sean x, y sucesiones reales. Franz Mertens demostró que si la serie
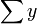 converge a Y y la serie
converge a Y y la serie 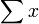 converge absolutamente a X entonces el producto de Cauchy de ellas
converge absolutamente a X entonces el producto de Cauchy de ellas 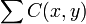 converge a XY. No es suficiente con que ambas series sean condicionalmente convergentes. Por ejemplo, la sucesión xn = ( − 1)n / n genera una serie condicionalmente convergente pero la sucesión C(x,x) no converge a 0. Ver la demostración a continuación.
converge a XY. No es suficiente con que ambas series sean condicionalmente convergentes. Por ejemplo, la sucesión xn = ( − 1)n / n genera una serie condicionalmente convergente pero la sucesión C(x,x) no converge a 0. Ver la demostración a continuación.Demostración del teorema de Mertens
Sea
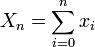 ,
, 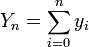 y
y 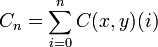 . Entonces
. Entonces 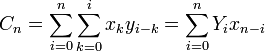 si se reordena. Por lo tanto
si se reordena. Por lo tanto 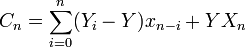 . Fijando un ε > 0. Dado que
. Fijando un ε > 0. Dado que 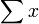 es absolutamente convergente y
es absolutamente convergente y 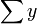 es convergente entonces existe un entero N tal que para todo
es convergente entonces existe un entero N tal que para todo 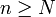
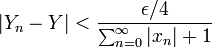 y un entero M tal que p[ara todo
y un entero M tal que p[ara todo 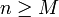
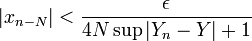 (dado que la serie converge, la sucesión debe converger a 0). También, existe un entero L tal que si
(dado que la serie converge, la sucesión debe converger a 0). También, existe un entero L tal que si 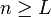 entonces
entonces 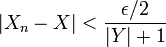 . Por lo tanto,
. Por lo tanto,para todos los enteros n mayores que N, M, y L. Por la definición de convergencia de una serie
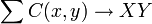 .
.Teorema de Cesàro
Si x e y son sucesiones reales y
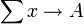 y
y 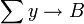 entonces
entonces 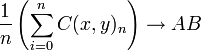
Generalizaciones
Todo lo enunciado en las secciones precedentes es aplicable a las sucesiones de números complejos
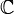 . Se puede definir también el producto de Cauchy para series en espacios euclídeos
. Se puede definir también el producto de Cauchy para series en espacios euclídeos 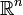 donde la multiplicación es el producto interno. En este caso, se verifica que si dos series convergen en forma absoluta entonces su producto de Cauchy converge en forma absoluta al producto interno de los límites.Categorías: Series matemáticas | Análisis complejo
donde la multiplicación es el producto interno. En este caso, se verifica que si dos series convergen en forma absoluta entonces su producto de Cauchy converge en forma absoluta al producto interno de los límites.Categorías: Series matemáticas | Análisis complejo
Wikimedia foundation. 2010.