- Problema de los dos cuerpos
-
Problema de los dos cuerpos
 Dos cuerpos orbitando alrededor de su centro de masas en órbitas elípticas.
Dos cuerpos orbitando alrededor de su centro de masas en órbitas elípticas.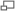
 Dos cuerpos con una pequeña diferencia de masa orbitando alrededor de su centro de masa, los tamaños dibujados son similares a los del sistema Plutón-Caronte.
Dos cuerpos con una pequeña diferencia de masa orbitando alrededor de su centro de masa, los tamaños dibujados son similares a los del sistema Plutón-Caronte.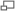
En mecánica, el problema de dos-cuerpos consiste en determinar el movimiento de dos partículas puntuales que sólo interactúan entre sí. Los ejemplos comunes incluyen la Luna orbitando la Tierra y en ausencia del Sol, es decir aislados, un planeta orbitando una estrella, dos estrellas que giran en torno al centro de masas (estrella binaria), y un electrón orbitando en torno a un núcleo atómico.
Como se explica más adelante, las Leyes de Newton nos permite reducir el problema de dos-cuerpos a un problema de un-cuerpo equivalente, es decir, a resolver el movimiento de una partícula sometida a un campo gravitatorio conservativo y que por tanto deriva de un potencial externo. Dado que el problema puede resolverse exactamente, el problema del dos-cuerpos correspondiente también puede resolverse con exactitud. Por el contrario, el problema de los tres cuerpos (y, más generalmente, el problema de n cuerpos con
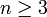 ) no puede resolverse, excepto en casos especiales.
) no puede resolverse, excepto en casos especiales.Contenido
Descripción del problema
Sean
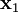 y
y 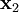 las posiciones de dos cuerpos, y m1 y m2 sus masas.
las posiciones de dos cuerpos, y m1 y m2 sus masas.La segunda ley de Newton determina que
donde
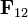 es la fuerza en masa 1 debido a su interacción con la masa 2, y
es la fuerza en masa 1 debido a su interacción con la masa 2, y 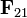 es la fuerza en masa 2 respecto a la masa 1.
es la fuerza en masa 2 respecto a la masa 1.Nuestra misión es determinar las trayectorias
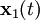 y
y 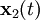 en todo instante t, dadas las posiciones iniciales
en todo instante t, dadas las posiciones iniciales 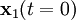 y
y 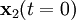 y las velocidades iniciales
y las velocidades iniciales 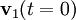 y
y 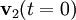 (12 constantes en total). Un truco importante para resolver el problema de dos-cuerpos es sumar y restar estas dos ecuaciones que descompone el problema en dos problemas. La suma produce una ecuación que describe el movimiento del centro de masas, y la resta da una ecuación que describe cómo varía con el tiempo el vector de posición entre las dos masas. Cuando combino las soluciones a éstos dos problemas de un-cuerpo obtengo las soluciones de las trayectorias
(12 constantes en total). Un truco importante para resolver el problema de dos-cuerpos es sumar y restar estas dos ecuaciones que descompone el problema en dos problemas. La suma produce una ecuación que describe el movimiento del centro de masas, y la resta da una ecuación que describe cómo varía con el tiempo el vector de posición entre las dos masas. Cuando combino las soluciones a éstos dos problemas de un-cuerpo obtengo las soluciones de las trayectorias 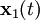 y
y 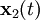 .
.Movimiento del centro de masas (Primer problema de un-cuerpo)
La suma de los dos ecuaciones
donde hemos usado Tercera Ley de Newton
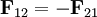 y donde
y dondees la posición del centro de masas (baricentro) del sistema. La ecuación resultante
muestra que la velocidad
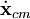 del centro de masa es constante, de lo que se deduce que la cantidad de movimiento total
del centro de masa es constante, de lo que se deduce que la cantidad de movimiento total 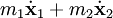 también es constante (conservación de la cantidad de movimiento). De modo que, pueden determinarse la posición y velocidad del centro de masa en cualquier instante dadas las posiciones y velocidades iniciales.
también es constante (conservación de la cantidad de movimiento). De modo que, pueden determinarse la posición y velocidad del centro de masa en cualquier instante dadas las posiciones y velocidades iniciales.Movimiento del vector de desplazamiento (Segundo problema de un-cuerpo)
Restando las dos ecuaciones de fuerza y reestructurando la ecuación
donde hemos usado de nuevo la Tercera ley de Newton
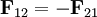 .
.
Nosotros introducimos un nuevo vector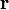
eso es el vector de posición de la masa 2 respecto a la masa 1. La fuerza entre los dos objetos sólo es una función de este vector de posición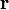 y no de sus posiciones absolutas
y no de sus posiciones absolutas 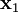 y
y 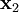 ; por otra parte, el problema no tendría simetría de translación, es decir, las leyes de la física cambiarían de un lugar a otro. Por consiguiente, la ecuación puede escribirse
; por otra parte, el problema no tendría simetría de translación, es decir, las leyes de la física cambiarían de un lugar a otro. Por consiguiente, la ecuación puede escribirsedonde μ es la masa reducida
Una vez que hemos resuelto las ecuaciones
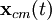 y
y 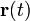 , las trayectorias originales pueden obtenerse de las ecuaciones
, las trayectorias originales pueden obtenerse de las ecuacionescomo puede verificarse por sustitución en las ecuaciones de definición de
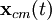 y
y 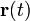 .
.El movimiento de dos-cuerpos es plano
El movimiento de dos cuerpos siempre está en un plano. Definamos la cantidad de movimiento
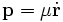 y el momento angular
y el momento angularLa variación con el tiempo del momento angular o cinético es igual al momento de fuerza
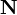
Como la fuerza entre las dos partículas está en la línea que las une y por tanto es paralela al radio vector
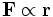 , el producto vectorial entre el vector de posición y la fuerza es nulo
, el producto vectorial entre el vector de posición y la fuerza es nulo 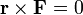 . Así que el momento es nulo y el momento angular o cinético es constante. Si el vector momento angular
. Así que el momento es nulo y el momento angular o cinético es constante. Si el vector momento angular 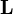 es constante, entonces, el vector de posición
es constante, entonces, el vector de posición 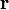 y su velocidad
y su velocidad 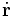 están siempre en el mismo plano, normal a
están siempre en el mismo plano, normal a 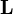 .
.Ley de las áreas
Es útil a menudo cambiar a las coordenadas polares, desde que el movimiento está en un plano y, para muchos problemas físicos, la fuerza
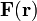 sólo es una función del radio r (es una fuerza central).
sólo es una función del radio r (es una fuerza central).Al moverse durante un instante de tiempo el vector de posición
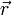 describe un área elemental
describe un área elemental 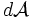 que vale:
que vale: 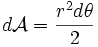 , así que la velocidad areolar o área barrida por el vector de posición en la unidad de tiempo es:
, así que la velocidad areolar o área barrida por el vector de posición en la unidad de tiempo es: 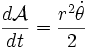 .
.El módulo del momento angular L = μr2ω donde
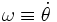 . Así que se puede expresar la velocidad areolar en función del momento angular
. Así que se puede expresar la velocidad areolar en función del momento angular 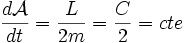 con
con 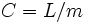 "constante de las áreas".
"constante de las áreas".Esta ley de las áreas fue enunciada empíricamente por primera vez en 1609 por Johannes Kepler y explica el movimiento de los planetas alrededor del Sol constituyendo la segunda ley de Kepler). Conviene recalcar que este hecho es una propriedad general del movimiento de las fuerzas centrales y es por tanto más general que las fuerzas de la gravitación inversamente proporcionales al cuadrado de la distancia.
El movimiento de un planeta en el plano de su órbita, se compone de dos movimientos, uno el ángulo que gira el radio vector y el otro su acercamiento o alejamiento del primario, es decir la variación del módulo del radio vector con el tiempo. La ley de las áreas determina que, un cuerpo gira más rápido cuando está cerca y lento cuando está lejos y lo hace cuantitativamente, como para poder establecer el ángulo de giro, aunque es difícil. Para obtener el ángulo de giro E con el tiempo hay que expresar está fórmula de otra manera:
Esta fórmula se denomina Ecuación de Kepler, donde M es la anomalía media, e es la excentricidad y E la anomalía excéntrica.
Sólo queda saber como varía r con el tiempo y eliminando t entre las dos euaciones obtener la órbita, pero esto es el tema de la siguiente sección.
La órbita
Newton dijo que "todo objeto en el universo atrae a otro objeto a lo largo de la línea que une el centro de los objectos, (fuerza central) proporcional a las masas de cada objeto, e inversamente proportional al cuadrado de la distancia entre ellos."
Por la segunda ley de Newton la aceleración a es de la forma
En coordenadas polares la velocidad, asumiendo que la órbita está en el plano OXY vale:
y la aceleración:
La aceleración en componentes y dado que sólo tiene componente radial:
Sustituyendo
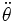 y
y 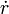 , la segunda ecuación queda:
, la segunda ecuación queda:Separando variables:
La integración resulta:
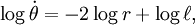 donde hemos añadido la constante de integración.
donde hemos añadido la constante de integración.
Sabemos que momento angular específico (por unidad de masa) vale:
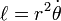 ,
,
Tomando logaritmos:
Trescientos años de experiencia avalan el cambio de variable:
Derivando:
Volviendo a derivar y teniendo presente que
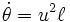
La ecuación de movimiento en
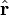
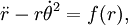 queda:
queda:
La ley de Newton de la gravitación indica que la fuerza por unidad de masa es:
donde G es la constante de gravitación universal y M es la masa de la estrella.
Resulta,
Esta ecuación diferencial tiene la solución general:
donde e and θ0 son constantes arbitrarias de integración.
Reemplazando u por 1/r y haciendo θ0 = 0:
Ésta es la ecuación de una cónica con excentricidad e y origen en un foco. Por tanto, la primera ley de Kepler es un resultado directo de la ley de la gravitación de Newton y de la segunda ley de Newton del movimiento.
θ recibe el nombre de anomalía verdadera normalmente se representa por V es el ángulo que forma el radio vector con el periastro y se relaciona fácilmente con la anomalía excéntrica E.
Véase también
- Leyes de Kepler
- Gravitación
- Teorema del Virial
- Problema de los tres cuerpos
- Problema de los n-cuerpos
Categoría: Mecánica celeste
Wikimedia foundation. 2010.

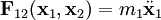
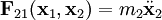
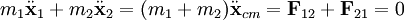
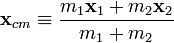
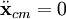
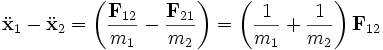
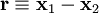
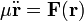
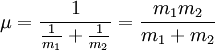
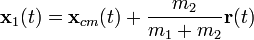
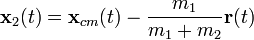
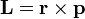
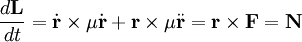
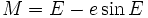
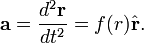
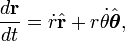
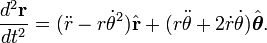
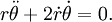
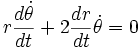
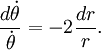
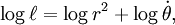
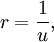
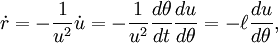
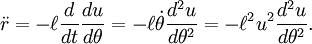
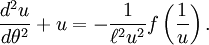
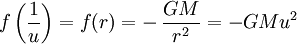
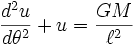
![u = \frac{GM}{\ell^2} \bigg[ 1 + e\cos(\theta-\theta_0) \bigg] .](/pictures/eswiki/50/241f8857608786f5f518ccddf31d2547.png)