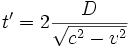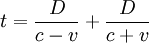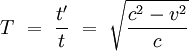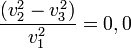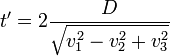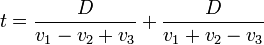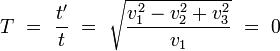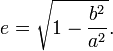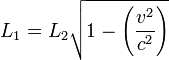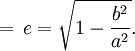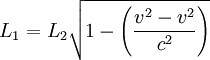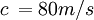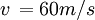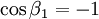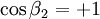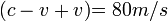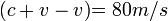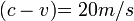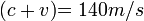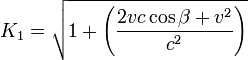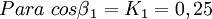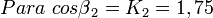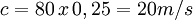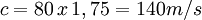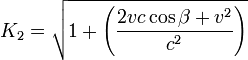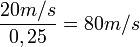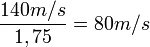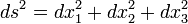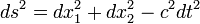- Analogía de Michelson y Morley
-
Analogía de Michelson y Morley
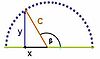
En la analogía de Michelson y Morley, dentro del experimento de Michelson y Morley, la figura representa a un río de anchura D, cuyas aguas fluyen a una velocidad constante «V», en donde la recta PQ (color rojo) represente el eje de las Y del plano cartesiano, y la recta PL (color azul) corresponde al eje de la X. Hay dos barcos, uno color amarillo (barco Y), y el otro de color verde (barco X). Ambos barcos parten simultáneamente desde el punto P del señalado río, los que viajan con la misma velocidad constante de «C»
El barco amarillo (barco Y) parte desde el punto P cruzando el río para llegar al punto Q, que se encuentra directamente opuesto al de la partida, a continuación desde Q regresa al punto P.
Simultáneamente a lo señalado precedentemente, el barco verde (barco X) recorre el río agua abajo hasta llegar al punto L, esto es, también recorre una distancia D; seguidamente desde L vuelve al punto P.
- BARCO Y: El observador se encuentra ubicado en tierra firme, esto es, está sentado en la silla que se posa en la ribera del río.
En el instante t 1, ambos barcos se encuentran ubicados en el punto P. Este es el único instante que es idéntico para ambos barcos.Consideremos en primer lugar lo correspondiente a la situación del barco amarillo (barco Y), tenemos que, si el referido barco enfila perpendicularmente a la corriente del río, la corriente lo arrastra aguas abajo alejándolo de su meta en la margen opuesta (punto Q). Para impedir aquello, deberemos neutralizar la velocidad «V», aplicando vectoriales, y así obtener la velocidad «B»
- BARCO X: en el caso del barco verde (barco X) la situación es algo diferente. Cuando navega agua abajo, su velocidad con respecto a la orilla es igual a la suma de su propia velocidad C más la de la velocidad V del río, y recorre la distancia D aguas abajo.
Sin embargo, en su viaje de vuelta, la velocidad del barco verde (barco X) con respecto de la orilla es igual a la diferencia entre su propia velocidad C y la velocidad V del río.
Pregunta: ¿Cuál es el tiempo necesario para cada recorrido completo?
- El tiempo empleado por el (barco Y) que se desplaza en ángulo recto, para Michelson y Morley es:
- El tiempo empleado por el (barco X) a favor de la corriente y contra corriente, según la interpretación de Michelson y Morley, estaría dado por:
- La diferencia en el tiempo sería:
Sin embargo, para responder tal interrogante, Michelson y Morley utilizaron un interferómetro propio, puesto que al realizar su experimento desestimaron, no solo el Interferómetro de Fizeau, sino que además las conclusiones y recomendaciones de Fizea, que demostraban que si los haces de luz viajaran por el aire atmosférico, resulta incorrecto utilizar la velocidad de la luz en el vacío c, ya que, en tal caso se debe usar la velocidad de la luz en el aire v. En donde, para el observador y el instrumento terrestre:
-
-
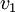 = velocidad de la luz en el aire.
= velocidad de la luz en el aire.
-
-
-
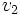 = velocidad del planeta Tierra.
= velocidad del planeta Tierra.
-
-
-
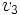 = velocidad del instrumento.
= velocidad del instrumento.
-
En tales condiciones, para el instrumento y el observador terrestre la velocidad de la luz, en el medio “aire”, siempre será la misma, cualquiera que sea la dirección y sentido en el que, los haces de luz, se desplacen en cada brazo del interferómetro de Michelson y Morley, lo que impide detectar la supuesta “variación de velocidad” que ellos equivocadamente supusieron podrían medir con su instrumento. En dicho experimento, la luz, viajó por el aíre adosado a la Tierra, y no por el Éter, que a aquellos investigadores les permitiría visualizar la adición de velocidades, o la diferencia de velocidad que la luz tendría en cada brazo del interferómetro.
- La diferencia en el tiempo sería:
¿Camino recto o sinusoidal?
 Trayectoria sinosuidal (arco de elipce)
Trayectoria sinosuidal (arco de elipce)
 Trayectoria:
Trayectoria:
1º).- Para un observado la trayectoria es recta.
2º).- Para el otro observado es sinosuidal.
3º).- En consecuencia lo correcto, es individualizar el marco de referencia, desde el cual se explica el acontecimiento físico.- En la analogía propuesta por Michelson y Morley, el (Barco Y) siguió un camino ¿recto o sinusoidal?
Algunos investigadores suponen que el "camino recto" seguido por el (barco Y), que le asignó la interpretación proporcionada por Michelson y Morley, correspondería a un desiderátum de aquellas personas que les agradaría mantener la creencia de que, Michelson y Morley, siguen teniendo la razón respecto de la interpretación del año 1887. Sin embargo - agregan los detractores - considerando que el ejemplo de los barcos tienen una trayectoria sinosuidal y no recta para el sistema de referencia terrestre, pero recta para el sistema de referencia exterior, y considerando que el experimento se realizó en el planeta Tierra, la trayectoria no podía ser recta. Sin olvidar, que la luz del interférómetro, es ajena al ejemplo de los barcos, dado que los haces de luz se desplazaban por el aire. En estas condiciones, con aire o con los barcos, la interpretación que se entregó estaría eventualmente equivocada.
Si r es la distancia instantánea desde Q al bote, en donde el ángulo beta es variable (∆), ya que beta es el ángulo dado en cada momento por r y PQ, y las aguas del río se mueven con la rapidez V; entonces, la trayectoria del bote no es la que indicaron Michelson y Morley a través de sus inadecuadas fórmulas, sino que, la trayectoria es el arco de una elipse que se visualiza por el observador situado en el marco de referencia
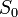 , según se gráfica a continuación:
, según se gráfica a continuación:Si la velocidad
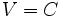 (10 m/min), y el ancho del río es de 14,142135 metros, entonces la trayectoria es un arco de la elipse, que en la figura aparece en color rojo.
(10 m/min), y el ancho del río es de 14,142135 metros, entonces la trayectoria es un arco de la elipse, que en la figura aparece en color rojo.Lo anterior acontecerá, siempre que el trazo se realice desde el sistema de referencia
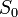 . Lo mismo debe acontecer para el barco.
. Lo mismo debe acontecer para el barco.- En un arranque unificador - sin un análisis serio ni en profundidad - alguien, para quedar bien con ambos bandos, podría livianamente valerse de un oxímoron literario e interpretar que, el camino recorrido por el (barco Y) es dual, es a la vez ambas cosas, y por lo mismo habría que considerarlo como una “trayectoria recta-sinusoidal”.
- Sin embargo, más que unificar se debe dejar de lado los sincretismos conciliadores, ya que aquello que efectivamente correspondería es hacer una disyunción, que separe esas dos realidades ¿Y cuál podría ser el algoritmo ad hoc para lograr esa desunión, para determinar cuándo y dónde, la trayectoria, se presenta de manera recta y cuándo de forma sinusoidal?.
Ese algoritmo consistiría en el método para detectar y diferenciar cuál es el “marcos de Referencia” para cada observador involucrado. Porque al parecer la trayectoria será “recta” o será “sinusoidal” dependiendo si el observador se encuentra ubicado o no en el sistema de referencia del medio material por el que transita la luz o está fuera de él. (Recordemos que aquí no estamos hablando de la luz que se desplaza en el vacío, sino de aquella que viaja a través de un medio material).¿Similitud de la vieja excentricidad con la moderna contracción de Lorentz?
A través de nuestro aporte, no es nuestra intención exterminar la interpretación de Michelson y Morley, o la de sus detractores; como tampoco es la de unificarlas en una sola. En consecuencia, aquí no pretendemos deslizar algún "elemento disociador" que conduzca al exterminio de alguna de ellas, ni menos, estamos aportando "elementos propios del sincretismo" que propicien la unificación de aquellas. Al contrario, con total honradez intelectual podemos asegurar que, nuestro intimo desiderátum (tíldese de realista, o utópico, o quimérico), es lograr la disyunción de ambas interpretaciones, enfrascándo, a cada una de ellas, dentro de su propia y justa perspectiva que, por lo demás, efectivamente le corresponde.
Por analogía, podemos señalar que si alguien describe un círculo; nos describe sus propiedades, y nos proporciona la ecuaciones matemáticas asociadas a ella, debemos entender que todas las explicaciones se encuentran circunscritas y referidas a un círculo; lo que obviamente no implica que no exista la elipse, como tampoco significa que la demostración de la existencia de un círculo pruebe la inexistencia de las elipses, o viceversa.
En consecuencia, si alguien constata que las formulas propias de un círculo, son inaplicables a una elipse, ello no significa necesariamente, que las elipses se encuentran derogadas por obsoletas.
De allí que resulte desafortunadas las palabras de Arthur Beiser, puesto que además conducen a la confusión de los alumnos que comienzan sus estudios sobre física clásica, física relativista, y física cuántica, ya que con esa clase de argumentos nos las presentan como antagónicas e irreconciliables, o lo que es peor, derogadas por obsoletas.
Sin embargo: ¿Cuál es el elemento per se que nos facultará para realizar la disyunción que nos permitirá separar dos cosas reales, como son los círculos y las elipses?
¡Sorpresa de las sorpresas!: el elemento per se para lograr la disyunción del circulo y la elipse, es nuestra vieja y querida Excentricidad, que a la vez, también sirve para la disyunción de la discusión que venimos examinando, la cual, en este último campo es más conocida como la Contracción de Lorentz, que a la vez es semejante a la relación de afinidad que proviene de la Circunferencia principal y de las correspondientes a la Apotema.
-
- La excentricidad e de una elipse de semieje mayor a y semieje menor b es:
-
- La Contracción de Lorentz e es:
Tanto la elipse como el círculo cuentan con dos focos, y ambos tienen excentricidad:- Focos:
-
- Los focos del círculo se encuentran en el mismo lugar en que está situado su centro.
- Los focos de la elipse se encuentra equidistante de su centro.
- Excentricidad:
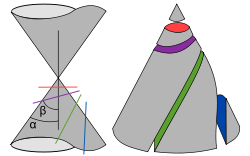
Tanto la "elipse" como el "círculo" provienen de la sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:
- β < α : Hipérbola (azul)
- β = α : Parábola (verde)
- β > α : Elipse (amarillo a la derecha, y morado a la izquierda)
- β = 90º : Circunferencia (rojo)
Con todos lo antecedentes ya proporcionados, procedamos, a través de un Gedankenexperiment (Experimento mental), a estirar una circunferencia; o la inversa a aplastar una elipse por su eje mayor:
En estas circunstancias, y casi por "arte de magia" transmutaremos dichas figuras: la circunferencia la transformaremos en una elipse, o la elipse en una circunferencia.
-
- ¿A qué apunta tanta metáfora, o si se quiere a tanta elucubración? Se ha efectuado tal preámbulo con la intención preconcebida de explicar la siguiente analogía:
- El círculo representa un marco de referencia, y la elipse otro diferente.
De allí surge el motivo por el cuál, para pasar del marco de referencia circular al marco de referencia elíptico, sea necesario recurrir a la vieja excentricidad, o a la olvidada relación de afinidad, o si se quiere a la moderna contracción de Lorentz.En efecto, la contracción de Lorentz representa el aplastamiento de la elipse que se hace por su eje mayor, para pasar del marco de referencia exterior al marco de referencia interior, en el cual, se realiza el experimento. O a la inversa, la mayor excentricidad del círculo, cuando éste se estira, representa pasar del marco de referencia interior al exterior.
En resumen, Michelson y Morley efectuaron su experimento dentro del "marco de referencia circular" pero interpretaron que lo estaban realizando en el "marco de referencia elíptico", en consecuencia para que las fórmulas matemáticas validas a un marco de referencia, tengan aplicación en el otro, es menester lo siguiente:
- Entonces la disyunción consiste en que:
-
- La Contracción de Lorentz, valida para el marco de referencia elíptico es:
-
- Y la Contracción de Lorentz, valida para el marco de referencia circular es:
-
- Ver además las fórmulas de la Apotema y a la vez, la relación de afinidad con la Circunferencia principal
Anamorfismo
La desfiguración de la circunferencia, al estirarla, que a la vez distorsiona el plano cartesiano asociado a aquella, se denomina anamorfosis, que corresponde a una perspectiva muy especial. El término anamorfosis se toma del griego que significa "trasformar".
El anamorfismo es una técnica en la que interviene las matemática, la óptica y el arte. La habilidad para representar la perspectiva se llevó al extremo en el siglo XVIII gracias a los conocimientos matemáticos que, a los artistas les permitió deformar la imagen, y luego, con determinados artilugios, les permitía reformarla a su estado original.
La anamorfosis corresponde a una técnica ingeniosa de perspectiva usada para entregar una imagen distorsionada del sujeto representado en una pintura cuando se ve desde el punto de vista usual, pero de tal manera distorsionada que si se ve desde un ángulo especial o si se refleja en un espejo curvo, la distorsión desaparece y la imagen en la pintura resulta normal.Los primeros ejemplos se encuentran en las notas de Leonardo da Vinci. Se consideraba un despliegue de virtuosismo técnico, y se incluía en la mayor parte de los manuales de dibujo de los siglos XVI y XVII. Dos ejemplos célebres son un retrato del rey Eduardo VI (1546, Galería Nacional de Retratos, Londres), atribuido a Cornelius Anthonisz, y una calavera al pie de los personajes.
En esta representación del siglo XII, que no tiene perspectiva matemática alguna, el castillo se encuentra empequeñecido por los guerreros. Los barcos, que se se supone se hallan muy distantes en el horisonte, parecen ser tan grandes comos los situados en primer término.
En medio de la fascinación por las matemáticas en la época del Renacimiento, los pintores empezaron a darse cuenta del importante papel que desempeñaba la geometría para alcanzar las perspectivas ópticas. Hasta entonces, la pintura había sido principalmente "conceptual". El término "perspectiva" deriva de la palabra latina "vista a través de" o "foco óptico.
Sin embargo el algoritmo y sus correspondientes ecuaciones matemáticas, para pasar de un dibujo con perspectiva a uno que no la tiene, o viceversa, son las que se insertan a continuación, y que se explica más adelante:- Los valores involucradosn en este ejemplo son:
- Para el Observador que viaja al interior del carro, no se adicionan la velocidad de la naranja con la velocidad del carro.
- Para el Observador que viaja al exterior del carro, se adicionan la velocidad de la naranja con la velocidad del carro.
- Factor
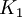 de transformación para que, el observador sin perpectiva, pueda calcular lo que visualizará el observador ubicado en el marco de referencia exterior:
de transformación para que, el observador sin perpectiva, pueda calcular lo que visualizará el observador ubicado en el marco de referencia exterior:
-
- En donde:
- Factor
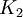 de transformación para que, el observador exterior, pueda calcular lo que visualizará el observador sin perspectiva:
de transformación para que, el observador exterior, pueda calcular lo que visualizará el observador sin perspectiva:
-
- En donde:
-
- Anamorfosis de la imagen de un perro:
Samuel Marolois recoge en su tratado de perspectiva de 1630 el método erróneo de Laurente publicado por Danti y lo aplica al siguiente dibujo de un perro.
Primero se ve el dibujo original cuadriculado, y después el mismo dibujo alargado en sentido horizontal en una proporción mayor de 3 a 1. Si miramos esta figura desde el lateral derecho con el ojo muy cerca del papel, observaremos que se produce un acortamiento de la figura en sentido horizontal y al mismo tiempo veremos converger hacia la izquierda las líneas horizontales de la cuadrícula, con lo que nunca se consigue una restitución total de la imagen original situada a la izquierda.
- La representación del espacio curvo de Bernhard Riemann.
El cuadro de la derecha en si está distorsionado por completo. Pero cuando se mira por un espejo en forma de tubo de quinqué las imágenes retornan a su forma normal. El artista, al pintar no mira directamente la realidad sino que lo hace guiado solamente por lo que se refleja en un espejo curvo.
Bernhard Riemann se ocupó de los espacios curvos. En dicho espacio se muestran las trayectorias más cortas entre puntos son líneas curvas, los triángulos se modifican al moverlos y la suma de sus ángulos interiores, en lugar de ser 180 grados, varía cuando los triángulos se trasladan.
Como consecuencia de lo anterior, la perspectiva ya no la podemos representar con estirar o contraer el plano cartesiano o espacio "plano clásico", para explicar la anamorfosis, como aconteció con la elipse y el círculo, y el perro, sino que debemos recurrir a las fórmulas de Bernhard Riemann, y nuevamente se soluciona el problema de pasar de una perspectiva plana a una curva, en donde el espacio se retuerce sobre sí mismo, etc.
La figura de la derecha gráfica la manera de pasar de un perspectiva curva y retorcida a una normal, ya que no debemos olvidar que las elipses, hipérbolas, parábolas y circunferencias, provienen de la misma cantera.
La Relatividad Especial usa tensores o cuadrivectores para definir un espacio no-euclídeo. Este espacio, sin embargo, es similar al espacio euclídeo tridimensional en muchos aspectos y es relativamente fácil trabajar en él. El diferencial de la distancia (ds) en un espacio euclídeo se define como:
Si se reducen las dimensiones espaciales a 2, se puede hacer una representación física en un espacio tridimensional,Se puede ver que las geodésicas con medida cero, si se extiende lo anterior a las tres dimensiones espaciales, las geodésicas nulas son esferas concéntricas, con radio = distancia = c*(+ o -)tiempo.
 El doble cono relativista, nos permite comprender la Relatividad Especial
El doble cono relativista, nos permite comprender la Relatividad Especial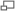
Nótese la gran similitud que existe entre entre los conos desde donde surgen las elipses, hipérbolas, parábolas y circunferencias, con el "doble cono" de distancias nulas representa el "horizonte de visión" de un punto en el espacio. Esto es, cuando se mira a las estrellas y se dice "La estrella de la que estoy recibiendo luz tiene X años.", se está viendo a través de esa línea de visión: una geodésica de distancia nula. Se está viendo un suceso a
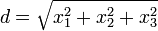 metros, y d/c segundos en el pasado. Por esta razón, el doble cono es también conocido como cono de luz. (El punto inferior de la izquierda del diagrama inferior representa la estrella, el origen representa el observador y la línea representa la geodésica nula, el "horizonte de visión" o cono de luz.) Es importante notar que sólo los puntos interiores al cono de luz del futuro de un evento pueden ser afectados causalmente por ese evento.
metros, y d/c segundos en el pasado. Por esta razón, el doble cono es también conocido como cono de luz. (El punto inferior de la izquierda del diagrama inferior representa la estrella, el origen representa el observador y la línea representa la geodésica nula, el "horizonte de visión" o cono de luz.) Es importante notar que sólo los puntos interiores al cono de luz del futuro de un evento pueden ser afectados causalmente por ese evento.¿Qué sucede cuándo se omite considerar una o más variables, y además el marco de referencia?
Supongamos que alguien desea investigar si efectivamente la Tierra gira sobre su eje, y además, si aquella se desplaza en torno al Sol. Y para elaborar su hipótesis, ese individuo, sigue el mismo "algoritmo" utilizado por Michelson y Morley, y por lo tanto omite considerar algunas de las variables y marcos de referencia que intervienen efectivamente, y, luego medita así:
- Si yo salto, sucederá que, mientras permanezco en el aire por n segundos, la Tierra - en ese mismo lapso - habrá girado y a la vez se habrá desplazado, por lo tanto, cuando yo vuelva a tocar nuevamente el suelo, necesariamente, caeré en un lugar diferente a aquel desde el que me impulsé para saltar, tal cual, se visualiza en la figura.
- Luego dota, para mantener en pie tanto su Hipótesis (método científico) como su figura esquemática, con un esqueleto de ecuaciones matemáticas.
- Sorpresa: el individuo ni sus instrumentos de medición pudieron detectar nada de lo que se predijó. Ese es el resultado del experimento: ¡nada de nada!
- El sujeto puede asignarle la siguiente interpretación al resultado entregado por sus instrumentos: "La Tierra no gira ni se desplaza".
Sin embargo, aquí acontecerá una curiosidad (a pesar de la errónea interpretación): Ni el resultado detectado, ni las ecuaciones usadas están equivocadas. Muy por el contrario, lo único equivocado será la interpretación asignada al resultado.En efecto, resulta que para el marco de referencia del individuo saltarín, ese resultado era lo que debía ser: la imposibilidad de detectar el giro y el traslado de la Tierra, no obstante, para un observado ubicado en un sistema de referencia ajeno a la Tierra, visualizará que la tierra gira y se desplaza.
- No olvidemos que las ecuaciones matemáticas son la forma, en donde, el fondo es la hipótesis, motivo por el cual, lo erróneo no son las ecuaciones, sino la hipótesis. Los siguientes ejemplos estarían demostrándolo:
Hesíodo, suponía que la Tierra estaba inmovilizada por “raíces infinitas” por cuya razón la esfera celeste no podía girar alrededor de la Tierra; en donde, la trayectoria del Sol consistía en una especie de movimiento pendular invertido (tal como hoy, vemos moverse la punta de los limpia parabrisas de un automóvil); esto es, cuando llegaba la noche, el Sol se apagaba y retrocedía sin iluminar camino hacia levante, para volverse a encender el día siguiente cuando iba iluminando de levante a poniente.
La posición en el plano cartesiano de cada punto, en su ubicación (x; y), de la trayectoria - en ese ir y venir - del sol de Hesiodo (desde 0 a 180, y de 180 a 0 grados, para el ángulo β), está dado por aplicación de las siguientes ecuaciones trigonométricas de la derecha:
Sin embargo, por ridícula y absurda que hoy nos parezca la hipótesis de Hesiodo, con algunos conocimientos matemáticos, la podemos dotar de un esqueleto de ecuaciones.
En efecto, fácil resultaría hacerlas, ya que, para ello bastaría con recurrir a las viajas pero vigentes fórmulas matemáticas aplicables al movimiento pendular propiamente tal.
Otro ejemplo lo constituye lo que aconteció en la España del siglo XIII, en donde el rey de Castilla Alfonso X, llamado el Sabio (partidario del sistema geocéntrico), organizó cerca de Toledo un observatorio, del que se valió para elaborar variadas ecuaciones matemáticas, a través de las cuales se explicara el movimiento de los cuerpos celestes alrededor de la Tierra inmóvil. Pero, esos movimientos de los astros cada día aparecían más complicados e inexplicables, y por ende era preciso introducir nuevas ecuaciones que representaran las nuevas esferas del firmamento y los nuevos movimientos a los astros al interior de esas esferas, con la finalidad de mantener invariable la inmovilidad de la Tierra.
A tal punto llegó esta complicación, que se asegura que el propio rey Sabio hubo de exclamar: “Si Dios me hubiese consultado cuando creó el Universo, le habría aconsejado hacerlo con mayor sencillez”.. Aquí también se utilizaron fórmulas matemática con las cuales se dotó a la hipótesis de la Tierra inmóvil (Geocentrismo)Consecuencias, de no diferenciar cuando un haz de luz se desplaza en el vacío o en un medio material
En palabras de Arthur Beiser
«Uno de los postulados de la relatividad especial establece que la velocidad de la luz C en el espacio libre es la misma para todos los observadores, independiente de su movimiento relativo. Pero el “sentido común” nos dice que si arrojamos hacia delante una pelota a 50 m/s desde un coche que se mueve a 80 m/s, la velocidad relativa de la pelota con respecto al suelo es de 130 m/s, igual a la suma de las dos velocidades. De que nos parezca que un rayo de luz emitido en un marco de referencia S1, en la dirección del movimiento de éste a la velocidad V con respecto a otro marco S2 deberá tener velocidades C + V en S2, lo cual está en contradicción con el postulado anterior. El “sentido común” no es más de fiar como guía en la ciencia que en cualquier dominio, y debemos recurrir a las ECUACIONES DE LA TRANSFORMACIÓN DE LORENTZ para obtener el esquema correcto de la suma de velocidades»
En palabras de Hermann Bondi:
-
- “En ciencia, no es útil suspirar por una información exhaustiva, sino que es menester trabajar con lo que se tiene y tratar de realizar la mejor tarea posible en el momento”. Por consiguiente, a pesar del enorme número de casos en que la teoría de Newton era correcta, ya no se la considera verdadera en ningún sentido. Pero, como la teoría de Newton es, matemáticamente, mucho más simple que la de Einstein, continuamos usándola como herramienta útil en la labor astronómica, pero como algo en cuya verdad no creemos, en ningún sentido de la palabra verdad”.
Si Herman Bondi, se sostiene en lo imposible, al desechar lo que dijo ser “verdadero” para usar lo supuestamente “falso”. Entonces, aunque aparezca improbable, deberemos suponer que eso que se dijo era “falso” es lo verdadero y lo que se declaró ser “verdadero” es lo falso; porque sino, trastoquemos todo, y así, la guerra debiera ser la paz, la libertad la esclavitud, Dios la maldad, el Demonio la bondad, y la ignorancia la fuerza.
Aquí no estamos criticando un oxímoron, ni un datismo, ni un pleonasmo literario de Bondi; sino que la evidente contradicción inserta en el mismísimo corazón de su conclusión.
Y como dijo el personaje Sherlock Holmes:-
- “Una vez que has excluido lo imposible, lo que queda, por improbable que parezca, debe ser la verdad”
Una cosa es el desplazamiento de la luz en el vacío, y una muy distinta, es el desplazamiento de la luz en un medio físico (aire, agua, vidrio, etc.), ya que si interviene un medio material, indefectiblemente no deberemos omitir los diferentes marcos de referencia.Nos es adecuado denigrar la vieja física por la nueva, ya que ambas son válidas, pero para su propio marco de referencia, como se demostrará más adelante.
Formula matemática einsteníana
Es posible que de conformidad con los argumentos expuestos, a más de algún lector, le haya surgido la inquietud de que aquí, solapadamente, se pretende inducir la idea de que Einstein pudiese estar equivocado. Al contrario, con dichos fundamentos se refuerza una vez más la validez que emerge de la conocida fórmula matemática einsteníana
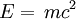 .
.Discusión:Analogía de Michelson y Morley
.
Marco de Referencia
Los detractores, sostienen que las fórmulas utilizadas por Michelson y Morley son válidas, exclusivamente, cuando el observador se encuentre fuera del planeta Tierra; ambos haces de luz del Experimento de Michelson y Morley se desplazaran por el vacío, y el interferómetro se encuentre en la Tierra. Esto es, que el experimento acontece en un Marco de Referencia distinto al que tiene el observador. Sin embargo muchas de estas condiciones no se dieron ni estaban presentes al momento de realizarse el experimento.
En la figura de la derecha, la Tierra gira, y con ella su atmósfera, también giran el interferómetro y el observador que se encuentran en la superficie terrestre, y además lo hace la luz que viaja por el aire atmosférico, lo que deja sin aplicación el esqueleto matemático elaborado para representar la interpretación asignada al resultado entregado por el experimento realizado por Michelson y Morley. Evento que se asemeja a la Aberración de la luz.
Una de las causas que falsea las posiciones de los astros es que la luz en un medio, no en el vacío, se desplaza con el medio que la transporta. Si gira la atmósfera conjuntamente con la Tierra, entonces el camino de la luz también gira divorciándose de la ubicación de la estrella desde donde llegó la luz a la atmósfera terrestre, y desde allí, la luz seguirá el giro de esa atmósfera adosada a la tierra. Desde luego, esto demuestra que la velocidad de la luz – cuando se desplaza en un medio material – es constante para el observador terrestre, pero no para el de otro marco de referencia.Ejemplo: Valores con objetos físicos
Los resultados que se obtienen desde diferentes marcos de referencia, nos recuerda la chistera de un mago, desde donde salen conejos, lugar en el que se suponía que no los habían.
En efecto, el observador ubicado al interior del carro visualiza que la naranja se desplaza a la misma velocidad, independiente que el carro se desplace a la derecha o a la izquierda.
Sin embargo, para el observador ubicado en el exterior (en el anden), esto es fuera del marco de referencia del pasajero, constatará que las velocidades de la naranja varían, o dicho de otra manera, se adicionan las velocidades.
- Los valores involucradosn en este ejemplo son:
- Para el Observador que viaja al interior del carro, no se adicionan la velocidad de la naranja con la velocidad del carro.
Situación que también se da con la luz que viaja adosada a la atmósfera terrestre, y nosotros, como pasajeros de este planeta, dado nuestro marco de referencia tampoco estamos en condiciones de visualizar esa adición de velocidades, de la que nos hablaron Michelson y Morley. Tampoco lo podrá detectar su interferómetro.- Para el Observador ubicado en el anden, ambas velocidades se suma o se restan dependiendo de la dirección y sentido en que, respecto de él, viaje el carro.
- Factor
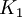 de transformación para que, el observador interior, pueda calcular lo que visualizará el observador ubicado en el marco de referencia exterior:
de transformación para que, el observador interior, pueda calcular lo que visualizará el observador ubicado en el marco de referencia exterior:
-
- En donde:
- Factor
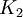 de transformación para que, el observador exterior, pueda calcular lo que visualizará el observador ubicado en el marco de referencia interior:
de transformación para que, el observador exterior, pueda calcular lo que visualizará el observador ubicado en el marco de referencia interior:
-
- En donde:
- Conclusiones:
Un observador situado fuera del marco de referencia terrestre, constatará que la velocidad de la luz, que viaja a través de un medio material, se adiciona a la velocidad de desplazamiento de ese medio.Si se pudiese lanzar al espacio una fibra óptica, de una longitud de un kilómetro, a una velocidad de 10.000 km/hora, la velocidad de la luz que viajaría en su interior se adicionaría a la velocidad de desplazamiento de la referida fibra. Sin se pudiese colocar un nano-instrumento al interior de la fibra, éste no podrá constatar la referida adición de velocidades.
En consecuencia, la dificultad que nubla la comprensión, consiste en omitir considerar los correspondientes marcos de referencia ya que «Ningún experimento mecánico, efectuado totalmente dentro de un sistema inercial, puede indicarle al observador cuál es el movimiento de dicho sistema con respecto a cualquier otro sistema inercial», excepto con un Péndulo o con un Giroscopio
Ejemplo: Valores con ondas sonoras
 A).- El observador que viaja a la intemperie puede constatar el Efecto Doppler, ya que el carro no arrastra consigo el aire.
A).- El observador que viaja a la intemperie puede constatar el Efecto Doppler, ya que el carro no arrastra consigo el aire.
 B).- El observador que viaja al interior de un carro cerrado, en el aire presurizado de la cabina, no podrá constatar el Efecto Doppler
B).- El observador que viaja al interior de un carro cerrado, en el aire presurizado de la cabina, no podrá constatar el Efecto Doppler
Ejemplo: Valores con ondas luminosas que se propagan en un medio físico
En las cuatro figuras el observador se encuentra en un marco de referencia diferente a la del río, en donde:
En tubo, adosado a la ribera del río, deja caer regletas de madera numeradas del uno al diez.
La velocidad del agua es de 10 m/s
El referido tubo, puede adquirir una velocidad de 0 a 10 m/s
- Ver figura A:
Si la velocidad del tubo es 0, entonces el observador ubicado sobre el puente, detecta que la velocidad de cada regleta es de 10 metros por minuto. Y las regletas hasta él llegan en secuencia (1, 2, 3, 4, 5,...n)
- Ver figura B:
Ahora, el tubo viaja hacia la izquierda.
El observador visualiza que las regletas mantienen su secuencia (1, 2, 3, 4, 5,...n), pero visualiza que la longitud de onda aumentó.
- Ver figura C:
En esta ocasión el tubo viaja hacia la derecha a una velocidad que no supera la velocidad del agua del río, por la que se desplazan las regletas.
El observador visualiza que en la longitud de onda se ha contraído. Sin embargo, la secuencia sigue siendo la misma (1, 2, 3, 4, 5,...n).
- Ver figura D:
En este nuevo evento, el tubo viaja hacia la derecha a una velocidad que supera la velocidad del agua del río, por la que se desplazan las regletas.
El observador visualiza que en la longitud de onda se ha contraído, pero si aumenta aún más la velocidad del tubo, verá que la longitud de onda han dejado de contraerse, sino que ellas irán en aumento. Empero, la secuencia de las regletas se invertirá (11, 10, 9, 8, 7,...n).
Y evidentemente que si la luz transporta información, esta llegará invertida, en donde los suceso primeros el observador los visualizará al final. Reiteremos una vez más que todos los ejemplos, ya expuestos, son válidos exclusivamente cuando la luz se desplaza a través de un medio, y no cuando ella viaja por el vacío.
Velocidad de la luz en un medio material
Referencias Externas
- Interferómetro de Fizeau
- Teoría de la relatividad: disputas de prioridad
- Apotema
- La analogía, desde la perspectiva de por otro autor
- Imagen del experimento en vivo
Categorías: Wikipedia:Fusionar | Experimentos físicos | Luz | Relatividad especial
Wikimedia foundation. 2010.