- Logaritmo binario
-
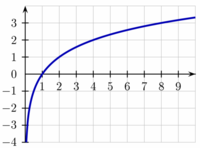
En matemática el logaritmo binario o logaritmo en base 2: y = log 2(x) es la función matemática que determina a que valor y hay que elevar 2 para obtener x, es un caso particular de logaritmos en el que la base es 2.
Esta base tiene su importancia en informática (donde se lo representa comúnmente como lg n, o ld n que proviene del Latín logarithmus dualis), dada la codificación binaria que se utiliza. Así por ejemplo con un número determinado de bits, ocho por ejemplo, se puede codificar una cantidad de información equivalente a 28 = 256, que es el número de variaciones que se pueden realizar con 0 y 1 en ocho posiciones. El uso del logaritmo binario, es útil cuando la información a calcular es la contraria: cuantas posiciones binarias y se necesitarán si se tiene que codificar x datos, direcciones, etc.
Con el ejemplo anterior para codificar 256 direcciones son necesarios log 2(256) = 8bits.
El logaritmo binario aparece frecuentemente en el análisis de algoritmos. Si un número n mayor que 1 es dividido por 2 repetidamente, el número de iteraciones necesitadas para obtener un valor de al menos 1 es la parte entera del lg n. Esta idea es utilizada en el análisis de varios algoritmos y estructura de datos. Por ejemplo en la búsqueda binaria, el tamaño del problema que resolver es dividido en mitades en cada iteración, y por lo tanto se necesitarán lg n iteraciones para resolver un problema de tamaño n. Similarmente, un árbol binario de búsqueda que contenga n elementos tiene una altura de lg n+1.
Contenido
Dominio y rango entero del Logaritmo binario
En dominio y rango entero, el logaritmo binario puede ser calculado con redondeo hacia arriba, o redondeo hacia abajo. Esas dos formas de logaritmos binarios enteros están relacionados a través de esta fórmula:
El siguiente código ejemplo para lenguaje C es un algoritmo para calcular el logaritmo binario (con redondeo hacia abajo) de un entero de 32 bits.[2] El operador '>>' representa un 'cambio no signado a la derecha'. La forma de redondear hacia abajo el logaritmo binario es idéntica a la forma de calcular la posición del bit 1 más significativo.
/** * Returns the floor form of binary logarithm for a 32 bit integer. * -1 is returned if n is 0. */ int floorLog2(unsigned int n) { int pos = 0; if (n >= 1<<16) { n >>= 16; pos += 16; } if (n >= 1<< 8) { n >>= 8; pos += 8; } if (n >= 1<< 4) { n >>= 4; pos += 4; } if (n >= 1<< 2) { n >>= 2; pos += 2; } if (n >= 1<< 1) { pos += 1; } return ((n == 0) ? (-1) : pos); }Utilizando calculadora
Una forma simple para calcular el log2(n) en una calculadora que no posee la función log2 es utilizar el logaritmo natural (base e, indicado como ln) o el logaritmo común (base 10, indicado como log), los cuales se encuentran en la mayoría de las calculadoras científicas. La fórmula para esto es:
Demostración
Para demostrar la relación anterior, partimos de:
que es lo mismo que:
tomando logaritmos:
por la propiedad de los logaritmos:
lo que resulta:
este resultado es independiente de la base de logaritmos que tomemos. Por lo que podemos generalizar:
Valor numérico
El valor numérico del logaritmo binario de un número real positivo puede ser calculado fácilmente utilizando este algoritmo escrito en lenguaje Python.[3]
#!/usr/bin/python from __future__ import division def log2(X): epsilon = 1.0/(10**12) integer_value=0 while X < 1: integer_value = integer_value - 1 X = X * 2 while X >= 2: integer_value = integer_value + 1 X = X / 2 decfrac = 0.0 partial = 0.5 X=X*X while partial > epsilon: if X >= 2: decfrac = decfrac + partial X = X / 2 partial = partial / 2 X=X*X return (integer_value + decfrac) if __name__ == '__main__': value = 4.5 print " X =",value print "LOG2(X) =",log2(value) # Ejemplo # # $ python log2.py # X = 4.5 # LOG2(X) = 2.16992500144 #Referencias
Véase también
Categorías:- Funciones especiales
- Logaritmos
Wikimedia foundation. 2010.