Función de Bessel

En matemática, las funciones de Bessel, primero definidas por el matemático Daniel Bernoulli y más tarde generalizadas por Friedrich Bessel, son soluciones canónicas y(x) de la ecuación diferencial de Bessel:

(1) $x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0$

donde α es un número real o complejo. El caso más común es cuando α es un entero n, aunque la solución para α no enteros es similar. El número α se denomina orden de las funciones de Bessel asociadas a dicha ecuación.

Dado que la ecuación anterior es una ecuación diferencial de segundo orden, tiene dos soluciones linealmente independientes.

Aunque α y − α dan como resultado la misma función, es convenión definir diferentes funciones de Bessel para estos dos parámetros, pues las funciones de Bessel en función del parámetro α son funciones suaves casi doquiera. Las funciones de Bessel se denominan también funciones cilíndricas, o armónicos cilíndricos porque son solución de la ecuación de Laplace en coordenadas cilíndricas.

Aplicaciones

La Ecuación de Bessel aparece cuando se buscan soluciones a la ecuación de Laplace o a la ecuación de Helmholtz por el método de separación de variables en coordenadas cilíndricas o esféricas. Por ello, las funciones de Bessel son especialmente importantes en muchos problemas de propagación de ondas, potenciales estáticos y cualquier otro problema descrito por las ecuaciones de Helmholtz o Laplace en simetrías cilíndricas o esféricas. Cuando se resuelven sistemas en coordenadas cilíndricas, se obtienen funciones de Bessel de orden entero (α = n) y en problemas resueltos en coordenadas esféricas, se obtienen funciones de Bessel de orden semientero (α = n + 1 / 2), por ejemplo:

• Ondas electromagnéticas en guías de onda cilíndricas.
• Modos transversales electromagnéticos en guías ópticas.
• Conducción del calor en objetos cilíndricos.
• Modos de vibración de una membrana delgada circular (o con forma de anillo).
• Difusión en una red.

También se usan funciones de Bessel en otro tipo de problemas como en procesado de señales.

Funciones de Bessel ordinarias

Las funciones de Bessel ordinarias de orden α, llamadas simplemente funciones de Bessel de orden α son soluciones de la ecuación de Bessel (1). Existen dos formas simples de expresar la solución general de la ecuación diferencial de Bessel con parámetro α, que están asociadas a las funciones de Bessel ordinarias de primera y de segunda especie.

Funciones de Bessel de primera especie: J_α

Las funciones de Bessel de primera especie y orden α son las soluciones de la ecuación diferencial de Bessel que son finitas en el origen (x = 0) para enteros no negativos α y divergen en el límite $x\rightarrow 0$ para α negativo no entero. El tipo de solución y la normalización de J_α(x) están definidos por sus propiedades abajo indicadas. Es posible definir la función J_α(x) por su expansión en serie de Taylor en torno a x = 0:^[1]

$J_\alpha(x) = \sum_{k=0}^\infty \frac{(-1)^k}{k! \Gamma(k+\alpha+1)} {\left({\frac{x}{2}}\right)}^{2k+\alpha} =\frac{x^\alpha}{2^\alpha\Gamma(\alpha+1)} \left[ 1-\frac{x^2}{2(2\alpha+2)}+\frac{x^4}{2\cdot4(2\alpha+2)(2\alpha+4)}-\ldots \right]$

Γ(z) es la función Gamma de Euler, una generalización del factorial para números complejos.

Estas funciones cumplen que:

• Si $\alpha\notin\mathbb{Z}$, entonces J_α(x) y J _{− α}(x) son linealmente independientes, y por tanto una solución general de la ecuación de Bessel puede expresarse como una combinación lineal de ellas.
• Si $\alpha = n\in\mathbb{Z}$, entonces se cumple:^[2]

$J_{-n}(x) = (-1)^{n} J_{n}(x), \quad \forall n\notin\mathbb{Z}$

por lo que las dos soluciones dejan de ser linealmente independientes. En este caso, la segunda solución linealmente independiente será una función de Bessel de segunda especie.

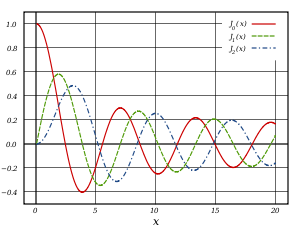
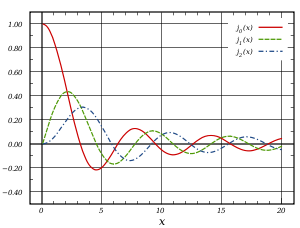
Las funciones de Bessel son funciones oscilatorias (como las funciones seno o coseno) que decaen proporcionalmente a $1/\sqrt{x}$ (como nos lo mostrarán las formas asintóticas de estas funciones más abajo), aunque los ceros de estas funciones no son, en general, periódicos, excepto de forma asintótica para grandes x.

Funciones de Bessel de primera especie, J_α(x), para órdenes enteros α=0,1,2.

Como casos particulares, se tienen las dos primeras funciones de Bessel enteras:

$J_0(x)= 1-\frac{x^2}{2^2}+\frac{x^4}{2^2 4^2}-\frac{x^6}{2^2 4^2 6^2}\ldots$

$J_1(x)= \frac{x}{2}-\frac{x^3}{2^2 4}+\frac{x^5}{2^2 4^2 6}-\frac{x^7}{2^2 4^2 6^2 8}\ldots$

$J'_0(x)= \frac{dJ_0(x)}{dx} = -J_1(x)$

Integrales de Bessel

Para valores enteros de n, se tiene la siguiente representación integral:

$J_n(x) = \frac{1}{\pi} \int_0^\pi \cos (n \tau - x \sin \tau) \,\mathrm{d}\tau.$

Que también se puede escribir como:

$J_n (x) = \frac{1}{2 \pi} \int_{-\pi}^\pi e^{-\mathrm{i}\,(n \tau - x \sin \tau)} \,\mathrm{d}\tau.$

Esta es la forma usada por Bessel en su estudio de estas funciones, y a partir de esta definicion dedujo varias propiedades de las mismas. Esta definición integral puede extenderse a órdenes no enteros añadiendo otro término integral:

$J_\alpha(x) = \frac{1}{\pi} \int_0^\pi \cos(\alpha\tau- x \sin\tau)\,d\tau - \frac{\sin(\alpha\pi)}{\pi} \int_0^\infty e^{-x \sinh(t) - \alpha t} \, dt.$

También se tiene, para $\alpha > -\frac{1}{2}$

$J_\alpha(x) = \frac{1}{\Gamma(\alpha + \frac{1}{2}) \sqrt{\pi}2^{\alpha-1}} \int_0^x (x^2-\tau^2)^{\alpha-\frac{1}{2}}\cos \tau \, d\tau.$

Relación con las series hipergeométricas

Las funciones de Bessel son un caso especial de función hipergeométrica

$J_\alpha(x)=\frac{(x/2)^\alpha}{\Gamma(\alpha+1)} \;_0F_1 (\alpha+1; -x^2/4).$

Esta fórmula está relacionada con la expansión de las funciones de Bessel en función de la función de Bessel–Clifford.

Relación con los polinomios de Laguerre

Las funciones de Bessel pueden expandirse en serie de polinomios de Laguerre L_k para cualquier parámetro t arbitrario como^[3]

$\frac{J_\alpha(x)}{\left( \frac{x}{2}\right)^\alpha}= \frac{e^{-t}}{\Gamma(\alpha+1)} \sum_{k=0} \frac{L_k^{(\alpha)}\left( \frac{x^2}{4 t}\right)}{{k+ \alpha \choose k}} \frac{t^k}{k!}.$

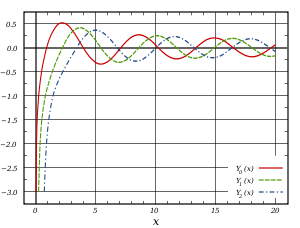
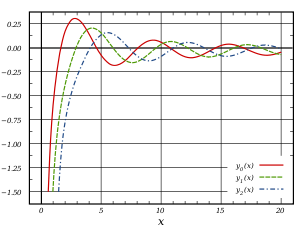
Funciones de Bessel de segunda especie: Y_α

Las funciones de Bessel de segunda especie, denotadas por Y_α(x), son soluciones de la ecuación diferencial de Bessel, Estas funciones divergen en el origen (x = 0).

Funciones de Bessel de segunda especie, Y_α(x), para órdenes α=0,1,2.

A estas funciones Y_α(x) también se les llama a veces funciones de Neumann o de Weber, y a veces se denotan por N_α(x). Para α; no enteros, se definen a partir de las funciones de primera especie J_α(x) mediante la siguiente fórmula:

$Y_\alpha(x) = \frac{J_\alpha(x) \cos(\alpha\pi) - J_{-\alpha}(x)}{\sin(\alpha\pi)}, \quad \forall\alpha\notin\mathbb{Z}$

En el caso en el que tengamos un orden entero n, la función es definida como el siguiente límite sólo válido para α no enteros:

$Y_n(x) = \lim_{\alpha \to n} Y_\alpha(x),\quad \forall n\in\mathbb{Z}$

que nos da el siguiente resultado en forma integral:

$Y_n(x) = \frac{1}{\pi} \int_{0}^{\pi} \sin(x \sin\theta - n\theta)d\theta - \frac{1}{\pi} \int_{0}^{\infty} \left[ e^{n t} + (-1)^n e^{-n t} \right] e^{-x \sinh t} dt$

Para el caso en el que tengamos α no enteros, la definición de Y_α(x) es redundante (como queda claro por su definición de arriba). Por otro lado, cuando α es entero, Y_α(x) es la segunda solucción linealmente independiente de la ecuación de Bessel, además, de forma similar a lo que ocurría con las funciones de primera especie, se cumple que:

$Y_{-n}(x) = (-1)^n Y_n(x) \forall n\in\mathbb{Z}$

Ambas J_α(x) y Y_α(x) son funciones holomorfas de x en el plano complejo cortado por el eje real negativo. Cuando α es un entero, no hay puntos de ramificación, y las funciones de Bessel son funciones enteras de x. Si fijamos x, entonces las funciones de Bessel son funciones enteras respecto a la variable α.

Funciones de Hankel: H_α⁽¹⁾, H_α⁽²⁾

Otra formulación importante de las dos solucciones linealmente independientes de la ecuación de Bessel son las funciones de Hankel $H_{\alpha}^{(1)}(x)$ y $H_{\alpha}^{(2)}(x)$ así definidas:^[4]

$\begin{matrix} H_{\alpha}^{(1)}(x) = J_{\alpha}(x) + i Y_{\alpha}(x) \\ H_{\alpha}^{(2)}(x) = J_{\alpha}(x) - i Y_{\alpha}(x) \end{matrix}$

donde i es la unidad imaginaria. Estas combinaciones lineales son también conocidas como las funciones de Bessel de tercera especie. Las funciones de Hankel de primera y segunda especie son usadas para representar las solucciones de ondas entrantes y salientes de una ecuación de ondas en simetrías cilíndricas respectivamente (o viceversa dependiendo de la convección de signo de la frecuencia). Estas funciones son así nombradas en honor de Hermann Hankel.

Usando la definición dada arriba, estas funciones se pueden escribir en función de las funciones de Bessel de primer orden J_α(x) así:

$\begin{matrix} H_{\alpha}^{(1)} (x) = \cfrac{J_{-\alpha} (x) - e^{-\alpha \pi i} J_\alpha (x)}{i \sin (\alpha \pi)}\\ H_{\alpha}^{(2)} (x) = \cfrac{J_{-\alpha} (x) - e^{\alpha \pi i} J_\alpha (x)}{- i \sin (\alpha \pi)} \end{matrix}$

Si α es un entero, se tiene que calcular de las expresiones de arriba así:

$\begin{matrix} H_{n}^{(1)}(x) = \lim_{\alpha \to n} H_{\alpha}^{(1)}(x)\forall n\in\mathbb{Z},\\ H_{n}^{(2)}(x) = \lim_{\alpha \to n} H_{\alpha}^{(2)}(x)\forall n\in\mathbb{Z}, \end{matrix}$

La siguiente relación es válida para todo valor de α, sea entero o no:^[5]

$\begin{matrix} H_{-\alpha}^{(1)} (x)= e^{\alpha \pi i} H_{\alpha}^{(1)} (x) \\ H_{-\alpha}^{(2)} (x)= e^{-\alpha \pi i} H_{\alpha}^{(2)} (x) \end{matrix}$

Existe una representación integral de las funciones de Hankel (útil para el cálculo de propagadores de la ecuación de Klein-Gordon):^[6]

$H_\alpha^{(1)} (x)= \frac{e^{-\frac{1}{2} \alpha\pi i}}{\pi i}\int_{-\infty}^{+\infty} e^{ix\cosh t - \alpha t} \, dt.$

$H_\alpha^{(2)} (x)= -\frac{e^{-\frac{1}{2} \alpha\pi i}}{\pi i}\int_{-\infty}^{+\infty} e^{-ix\cosh t - \alpha t} \, dt.$

Solución general de la ecuación de Bessel

La solución general de la ecuación diferencial de Bessel con parámetro α viene dada en términos de las funciones de Bessel ordinarias o de las funciones de Hankel. Dicha solución general puede expresarse como:

(2) $\begin{cases} y(x) = AJ_{\alpha}(x)+BJ_{-\alpha}(x) & \forall\alpha \notin \mathbb{Z} \\ y(x) = AJ_{\alpha}(x)+BY_{\alpha}(x) & \forall \alpha \in \mathbb{R} \\ y(x) = AJ_{\alpha}(x)+BJ_{\alpha}(x)\int\cfrac{dx}{xJ_{\alpha}^2(x)} & \forall \alpha \in \mathbb{R} \\ y(x) = AH_{\alpha}^{(1)}(x)+BH_{\alpha}^{(2)}(x) & \forall\alpha \in \mathbb{R} \end{cases}$

Donde A y B son dos constantes arbitrarias.

Funciones de Bessel modificadas: I_α, K_α

Las funciones de Bessel ordinarias son válidas para valores complejos del argumento x, y un caso especialmente importante es aquel con argumento imaginario puro. En este caso, la ecuación de Bessel se transforma en la ecuación de Bessel modificada^[7]

(3) $x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} - (x^2 + \alpha^2)y = 0,$

y sus dos soluciones linealmente independientes son las funciones de Bessel modificadas de primer y segundo tipo: I_α(x) y K_α(x) respectivamente.^[8]

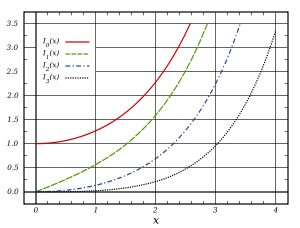
Funciones de Bessel modificadas de primera especie: I_α

Las funciones de Bessel modificadas de primera especie y orden α vienen dadas por:

$I_\alpha(x)= \sum_{k=0}^\infty \frac{1}{k!\Gamma(k+\alpha+1)}\left(\frac{x}{2}\right)^{2k+\alpha}=\frac{x^\alpha}{2^\alpha\Gamma(\alpha+1)} \left[ 1+\frac{x^2}{2(2\alpha+2)}+\frac{x^4}{2\cdot4(2\alpha+2)(2\alpha+4)}+\ldots \right]$

Están relacionadas con las funciones de Bessel ordinarias mediante la siguiente igualdad:

$I_\alpha(x) = i^{-\alpha}J_\alpha(ix) = e^{-\alpha\pi i/2}J_\alpha(ix)\;$.

• Si $\alpha\notin\mathbb{Z}$ entonces I_α(x) y I _{− α}(x) son linealmente independientes, y por tanto dan una solución general de la ecuación de Bessel.
• Si $\alpha\notin\mathbb{Z}$ entonces J _{− α}(x) no está definida en x = 0.

Casos particulares:

$I_0(x)= 1+\frac{x^2}{2^2}+\frac{x^4}{2^2 4^2}+\frac{x^6}{2^2 4^2 6^2}\ldots$

$I_1(x)= \frac{x}{2}+\frac{x^3}{2^2 4}+\frac{x^5}{2^2 4^2 6}+\frac{x^7}{2^2 4^2 6^2 8}\ldots$

$I'_0(x)= \frac{dI_0(x)}{dx} = I_1(x)$

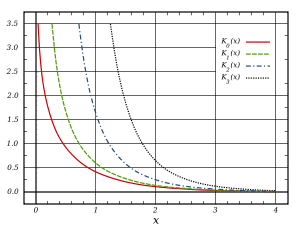
Funciones de Bessel modificadas de segunda especie: K_α

Las funciones de Bessel modificadas de segunda especie y orden α se definen a partir de las funciones modificadas de primera especie para órdenes no enteros mediante las siguiente fórmula:

$K_{\alpha}(x) = \frac{\pi}{2} \frac{I_{-\alpha} (x) - I_\alpha (x)}{\sin (\alpha \pi)} \forall \alpha\notin\mathbb{Z}$

Para los casos en los que α sea entero ($\alpha = n\in\mathbb{Z}$), tenemos que tomar el límite del orden no entero al entero así:

$K_{n}(x) = \lim_{p\rightarrow n}K_{p}(x) = \lim_{p\rightarrow n}\frac{\pi}{2} \frac{I_{-p}(x) - I_{p}(x)}{\sin(p\pi)} \forall n\in\mathbb{Z}$

Además se puede escribir esta función a partir de la función de Hankel de primera especie así:

$K_{\alpha}(x) = \frac{\pi}{2} i^{\alpha+1} H_{\alpha}^{(1)}(ix) = -\frac{\pi}{2} i^{\alpha+1} e^{-i \pi \alpha} H_{\alpha}^{(2)}(-ix).$

Existen varias representaciones integrales de estas funciones. La siguiente de K_α (x) es útil para el cálculo del propagador de Feynman en Teoría Cuántica de Campos:

$K_\alpha(x) = \frac{1}{2} e^{-\frac{1}{2}\alpha\pi i} \int_{-\infty}^{+\infty} e^{-ix\sinh t -\alpha t} dt$

Las funciones de Bessel modificadas de segunda especie han sido también llamadas:

• Funciones de Basset
• Funciones de Bessel modificadas de tercera especie
• Funciones de MacDonald
• Funciones de Hankel modificadas^[9]

Al contrario que las funciones de Bessel ordinarias, J_α and Y_α, las cuales son funciones oscilatorias para argumentos reales, las funciones de Bessel modificadas, I_α and K_α, son exponencialmente creciente y decreciente respectivamente. Como la función de Bessel ordinaria J_α, la función I_α va a cero en x = 0 para α > 0 y es finita en x = 0 para α = 0. Análogamente, K_α diverge en x = 0.

Función de Bessel modificada de primera especie, Iα(x), para α=0,1,2,3.

Función de Bessel modificada de segunda especie, Kα(x), para α=0,1,2,3.

Solución general de la ecuación de Bessel modificada

La solución general de la ecuación diferencial de Bessel modificada con parámetro α viene dada por:

(4) $\begin{cases} y(x) = AI_\alpha(x)+BI_{-\alpha}(x) & \alpha \notin \mathbb{Z} \\ y(x) = AI_\alpha(x)+BK_{\alpha}(x) & \forall \alpha \in \mathbb{R} \\ y(x) = AI_\alpha(x)+BI_{\alpha}(x)\int\cfrac{dx}{xI_\alpha^2(x)} & \forall \alpha \in \mathbb{R} \end{cases}$

Donde A y B son dos constantes arbitrarias.

Funciones esféricas de Bessel: j_n,y_n

Funciones esféricas de Bessel de primer orden, j_n(x), para n=0,1,2.

Funciones esféricas de Bessel de segundo orden, y_n(x), para n=0,1,2.

Cuando se solucciona la ecuación de Helmholtz en coordenadas esféricas por separación de variables, la ecuación radial tiene la forma:

$x^2 \frac{d^2 y}{dx^2} + 2x \frac{dy}{dx} + [x^2 - n(n+1)]y = 0.$

Donde n es un entero positivo. Las dos solucciones linealmente independientes de esta ecuación se denominan funciones esféricas de Bessel j_n(x) y y_n(x), y están relacionadas con las funciones de Bessel ordinarias J_n(x) y Y_n(x) por:^[10]

$j_n(x) = \sqrt{\frac{\pi}{2x}} J_{n+1/2}(x),$

$y_n(x) = \sqrt{\frac{\pi}{2x}} Y_{n+1/2}(x) = (-1)^{n+1} \sqrt{\frac{\pi}{2x}} J_{-n-1/2}(x).$

y_n se escribe también como n_n o η_n. A esta función a veces se le llama función esférica de Neumann.

Las funciones esféricas de Bessel se pueden obtener a partir de las siguientes fórmulas:

$j_n(x) = (-x)^n \left(\frac{1}{x}\frac{d}{dx}\right)^n\,\frac{\sin x}{x} ,$

$y_n(x) = -(-x)^n \left(\frac{1}{x}\frac{d}{dx}\right)^n\,\frac{\cos x}{x}.$

La función de Bessel esférica j₀(x) es la Función sinc desnormalizada.

Para n = 0,1 y 2 tenemos:^[11]

$j_0(x)=\frac{\sin x} {x}$

$j_1(x)=\frac{\sin x} {x^2}- \frac{\cos x} {x}$

$j_2(x)=\left(\frac{3} {x^2} - 1 \right)\frac{\sin x}{x} - \frac{3\cos x} {x^2}$^[12]

$j_3(x)=\left(\frac{15}{x^3} - \frac{6}{x} \right)\frac{\sin x}{x} -\left(\frac{15}{x^2} - 1\right) \frac{\cos x} {x},$

$y_0(x)=-j_{-1}(x)=-\,\frac{\cos x} {x}$

$y_1(x)=j_{-2}(x)=-\,\frac{\cos x} {x^2}- \frac{\sin x} {x}$

$y_2(x)=-j_{-3}(x)=\left(-\,\frac{3}{x^2}+1 \right)\frac{\cos x}{x}- \frac{3 \sin x} {x^2};$

La fórmula general es:

$J_{n+\frac 1 2}(x)=\sqrt \frac 2 {\pi x} \sum_{i=0}^\frac {n+1} 2 (-1)^{n-i}\left[\sin(x) \left(\frac 2 x\right)^{n-2i} \frac {(n-i)!}{i!} {-\frac 1 2-i \choose n-2i}- \cos(x) \left(\frac 2 x\right)^{n+1-2i} \frac {(n-i)!}{i!} i {-\frac 1 2-i \choose n-2i+1}\right].$

Funciones de Hankel esféricas: h _n

Las funciones esféricas de Hankel se definen de forma análoga a las no esféricas:

$h_{n}^{(1)}(x) = j_{n}(x) + i y_{n}(x)$

$h_{n}^{(2)}(x) = j_{n}(x) - i y_{n}(x).$

De hecho, esto nos dice que existen expresiones cerradas de las funciones de Bessel de orden semientero en término de funciones trigonométricas y, por tanto, también de las funciones esféricas de Bessel. De esto se deduce que, para n entero no negativo se tiene:

$h_{n}^{(1)}(x) = (-i)^{n+1}\frac{e^{ix}}{x}\sum_{m=0}^{n}\frac{i^{m}}{m!(2x)^{m}}\frac{(n+m)!}{(n-m)!}$

y $h_n^{(2)}$ es la función compleja conjugada de esta (para x real). De esta fórmula se pueden deducir las formas cerradas de las funciones esféricas de Bessel ordinarias, por ejemplo, j₀(x) = sin(x) / x y y₀(x) = − cos(x) / x, y así para cualquier argumento n.

Funciones esféricas de Bessel modificadas: i_n,k_n

También existen análogos esféricos de las funciones de Bessel modificadas:

$i_{n}(x) = \sqrt{\frac{\pi}{2x}} I_{n+1/2}(x) = i^{-n}j_{n}(ix)\;$.

$k_{n}(x) = \sqrt{\frac{\pi}{2x}} K_{n+1/2}(x) = \frac{\pi}{2} i^{n} h_{n}^{(1)}(ix) \!$

k_n(x) se pueden escribir de forma cerrada, usando la fórmula de $h_{n}^{(1)}(x)$ dada arriba como:

$k_{n}(x) = \frac{\pi}{2} \frac{e^{-x}}{x}\sum_{m=0}^{n}\frac{(n+m)!}{m!(n-m)!}\frac{1}{(2x)^{m}}$

Función generatriz

Se pueden obtener las funciones de Bessel esféricas a partir de las siguientes funciones generatrices:^[13]

$\frac 1 {z} \cos \sqrt{z^2 - 2zt}= \sum_{n=0}^\infty \frac{t^n}{n!} j_{n-1}(z),$

$\frac 1 {z} \sin \sqrt{z^2 + 2zt}= \sum_{n=0}^\infty \frac{(-t)^n}{n!} y_{n-1}(z) .$

Relaciones diferenciales

La siguiente relación diferencial se cumple para $f_{n}(z) = \{j_{n}(z), y_{n}(z), h_{n}^{(1)}(z), h_{n}^{(2)}(z)\}\, \forall n\in\mathbb{Z}$

$\left(\frac{1}{z}\frac{d}{dz}\right)^m\left(z^{n+1}f_n(z)\right)=z^{(n-m)+1}f_{(n-m)}(z).$

Funciones de Riccati-Bessel: S_n,C_n,ξ_n,ζ_n

Las funciones de Riccati-Bessel son una pequeña modificación de las funciones de Bessel esféricas:

$S_{n}(x)=x j_{n}(x)=\sqrt{\pi x/2}J_{n+1/2}(x)$

$C_{n}(x)=-x y_{n}(x)=-\sqrt{\pi x/2}Y_{n+1/2}(x)$

$\xi_{n}(x) = x h_{n}^{(1)}(x)=\sqrt{\pi x/2} \, H_{n+1/2}^{(1)}(x)=S_{n}(x)-iC_{n}(x)$

$\zeta_{n}(x)=x h_{n}^{(2)}(x)=\sqrt{\pi x/2}H_{n+1/2}^{(2)}(x)=S_{n}(x)+iC_{n}(x)$

Estas funciones satisfacen la siguiente ecuación diferencial:

$x^2 \frac{d^{2}y}{dx^{2}} + [x^{2} - n(n+1)]y = 0$

Esta ecuación diferencial y sus soluciones, las ecuaciones de Riccati-Bessel, se usan para resolver el problema de scattering de ondas electromagnéticas por una esfera, problema conocido como scattering de Mie tras la publicación por vez primera de estos resultados por Mie en 1908. Véase por ejemplo, Du (2004).^[14]

Según Debye (1909) se usa a veces la notación ψ_n,χ_n en vez de S_n,C_n.

Expansiones asintóticas

Las funciones de Bessel tienen las siguientes expansiones asintóticas para α no negativos. Para pequeño argumento $0 < x \ll \sqrt{\alpha + 1}$, se tiene:^[15]

$J_\alpha(x) \approx \frac{1}{\Gamma(\alpha+1)} \left( \frac{x}{2} \right) ^\alpha$

$Y_\alpha(x) \approx \left\{ \begin{matrix} \frac{2}{\pi} \left[ \ln (x/2) + \gamma \right] & \mbox{si } \alpha=0 \\ \\ -\frac{\Gamma(\alpha)}{\pi} \left( \frac{2}{x} \right) ^\alpha & \mbox{si } \alpha > 0 \end{matrix} \right.$

donde γ es la constante de Euler-Mascheroni y Γ(x) es la función Gamma de Euler. Como aproximación asintótica al infinito, (cuando tenemos un argumento tal que verifica $x \gg |\alpha^2 - 1/4|$), se obtienen las siguientes aproximaciones:^[15]

$J_\alpha(x) \approx \sqrt{\frac{2}{\pi x}} \cos \left( x-\frac{\alpha\pi}{2} - \frac{\pi}{4} \right)$

$Y_\alpha(x) \approx \sqrt{\frac{2}{\pi x}} \sin \left( x-\frac{\alpha\pi}{2} - \frac{\pi}{4} \right).$

Para α=1/2 estas fórmulas son exactas. Las expansiones asintóticas del resto de funciones de Bessel se obtienen a partir de las mostradas arriba y de sus relaciones con las funciones de Bessel de primera especie. Así, las aproximaciones asintóticas al infinito de las funciones de Bessel modificadas (es decir, para argumentos x que verifiquen $x \gg |\alpha^2 - 1/4|$) se tiene:

$I_\alpha(x) \approx \frac{e^x}{\sqrt{2\pi x}} \left(1+ \frac{(1-2 \alpha)(1+2\alpha)}{8x}+ \cdots \right) ,$

$K_\alpha(x) \approx \sqrt{\frac{\pi}{2x}} e^{-x}.$

Mientras que el límite de muy bajo argumento, $0 < x \ll \sqrt{\alpha + 1}$, se obtiene:

$I_\alpha(x) \approx \frac{1}{\Gamma(\alpha+1)} \left( \frac{x}{2} \right) ^\alpha$

$K_\alpha(x) \approx \left\{ \begin{matrix} - \ln (x/2) - \gamma & \mbox{si } \alpha=0 \\ \\ \frac{\Gamma(\alpha)}{2} \left( \frac{2}{x} \right) ^\alpha & \mbox{si } \alpha > 0 \end{matrix} \right.$

Propiedades

Para enteros de orden α = n, J_n(x) se puede definir a partir de la serie de Laurent de la siguiente función generatriz:

$e^{(x/2)(t-1/t)} = \sum_{n=-\infty}^\infty J_n(x) t^n,$

aproximación tomada por P. A. Hansen en 1843. Esta expresión puede generalizarse a órdenes no enteros usando integración de contorno u otros métodos. Otra expresión importante para órdenes enteros es la identidad de Jacobi-Anger:

$e^{iz \cos \phi} = \sum_{n=-\infty}^\infty i^n J_n(z) e^{in\phi},$

identidad que es usada para expandir ondas planas en una serie infinita de ondas cilíndricas o para encontrar la serie de Fourier de un tono de una señal de FM.

Más generalmente, una función ƒ se puede expandir en una serie de la forma

$f(z)=a_0^\nu J_\nu (z)+ 2 \cdot \sum_{k=1} a_k^\nu J_{\nu+k}(z),$

que se denomina expansión de Neumann de ƒ. Los coeficientes de esta serie en el caso ν = 0 tienen la siguiente forma explícita

$a_k^0=\frac{1}{2 \pi i} \int_{|z|=c} f(z) O_k(z) \, \mathrm d z,$

donde O_k son los polinomios de Neumann.^[16]

Existen funciones que admiten la siguiente representación especial

$f(z)=\sum_{k=0} a_k^\nu J_{\nu+2k}(z)$

con

$a_k^\nu=2(\nu+2k) \int_0^\infty f(z) \frac{J_{\nu+2k}(z)}z \mathrm d z$

debido a la rtelación de ortogonalidad

$\int_0^\infty J_\alpha(z) J_\beta(z) \frac {\mathrm d z} z= \frac 2 \pi \frac{\sin\left(\frac \pi 2 (\alpha-\beta) \right)}{\alpha^2 -\beta^2}.$

Más generalmente, si f tiene un punto de ramificación donde

f(z) =	∑	akJν + k(z),
	k = 0

entonces

No se pudo entender (La conversión a PNG ha sido errónea): \mathcal L \left\{\sum_{k=0} a_k J_{\nu+k} \right\}(s)= \frac 1 \sqrt{1+s^2} \sum_{k=0} \frac{a_k}{(s+\sqrt{1+s^2})^{\nu+k}}

o

$\sum_{k=0} a_k \xi^{\nu+k}= \frac{1+\xi^2}{2\xi} \mathcal L \{f \} \left( \frac{1-\xi^2}{2\xi} \right),$

donde $\mathcal L \{f \}$ es la transformada de Laplace de ƒ.^[17]

Otra manera de definir las funciones de Bessel son la representación de Poisson y la fórmula de Mehler-Sonine:

$\begin{align}J_\nu(z) &= \frac{ (\frac{z}{2})^\nu }{ \Gamma(\nu + \frac{1}{2} ) \sqrt{\pi} } \int_{-1}^{1} e^{izs}(1 - s^2)^{\nu - \frac{1}{2} } ds, \\ &=\frac 2{{\left(\frac z 2\right)}^\nu\cdot \sqrt{\pi} \cdot \Gamma\left(\frac 1 2-\nu\right)} \int_1^\infty \frac{\sin(z u)}{(u^2-1)^{\nu+\frac 1 2}} d u,\end{align}$

donde ν > −1/2 y z es un número complejo.^[18] Esta fórmula es especialmente útil cuando se trabaja con transformadas de Fourier.

Las funciones J_α(x), Y_α(x), $H_{\alpha}^{(1)}(x)$ y $H_{\alpha}^{(2)}(x)$ cumplen las siguientes relaciones de recurrencia:

$\frac{2\alpha}{x} Z_\alpha(x) = Z_{\alpha-1}(x) + Z_{\alpha+1}(x)$

$2\frac{dZ_\alpha}{dx} = Z_{\alpha-1}(x) - Z_{\alpha+1}(x)$

Donde Z denota J, Y, H⁽¹⁾, o H⁽²⁾.

Estas dos identidades se suelen combinar para obtener otras relaciones distintas. Por ejemplo, se pueden calcular funciones de Bessel de mayores órdenes (o mayores derivadas) a partir de funciones de Bessel de menor orden o de derivadas de menor orden. En particular, se cumple:

$\left( \frac{d}{x dx} \right)^m \left[ x^\alpha Z_{\alpha} (x) \right] = x^{\alpha - m} Z_{\alpha - m} (x)$

$\left( \frac{d}{x dx} \right)^m \left[ \frac{Z_\alpha (x)}{x^\alpha} \right] = (-1)^m \frac{Z_{\alpha + m} (x)}{x^{\alpha + m}}$

Las funciones modificadas de Bessel cumplen relaciones similares:

$e^{(x/2)(t+1/t)} = \sum_{n=-\infty}^\infty I_n(x) t^n,$

$e^{z \cos \theta} = I_0(z) + 2\sum_{n=1}^\infty I_n(z) \cos(n\theta),$

Las relaciones de recurrencia serán en este caso:

$C_{\alpha-1}(x) - C_{\alpha+1}(x) = \frac{2\alpha}{x} C_\alpha(x)$

$C_{\alpha-1}(x) + C_{\alpha+1}(x) = 2\frac{dC_\alpha}{dx}$

donde C_α denotará a I_α o a e^απiK_α. Estas relaciones son útiles para problemas de difusión discreta.

La división de la ecuación de Bessel por x es una ecuación hermítica o auto-adjunta, por lo que sus solucciones deben cumplir determinadas relaciones de ortogonalidad para unas condiciones de contorno adecuadas. En particular, se cumple:

$\int_0^1 x J_\alpha(x u_{\alpha,m}) J_\alpha(x u_{\alpha,n}) dx = \frac{\delta_{m,n}}{2} [J_{\alpha+1}(u_{\alpha,m})]^2 = \frac{\delta_{m,n}}{2} [J_{\alpha}'(u_{\alpha,m})]^2,$

donde α > − 1, δ_n,m es la delta de Kronecker, y u_α,m es el m-ésimo cero de J_α(x). Esta relación de ortogonalidad puede ser usada para extraer coeficientes de las series de Fourier-Bessel, donde una función se expande en una base de funciones de Bessel J_α(xu_α,m) para α fijo y m variable. (Obtener una relación análoga para funciones de Bessel esféricas es trivial.)

Se puede obtener de forma inmediata una relación análoga para funciones de Bessel esféricas:

$\int_0^1 x^2 j_\alpha(x u_{\alpha,m}) j_\alpha(x u_{\alpha,n}) dx = \frac{\delta_{m,n}}{2} [j_{\alpha+1}(u_{\alpha,m})]^2$

Otra relación de ortogonalidad es la ecuación de cierre:

$\int_0^\infty x J_\alpha(ux) J_\alpha(vx) dx = \frac{1}{u} \delta(u - v)$

para α > − 1 / 2 y siendo δ(x) la función delta de Dirac. Esta propiedad se usa para construir expansiones de funciones arbitrarias como series de funciones de Bessel mediante la transformada de Hankel.

Para funciones de Bessel esféricas, la relación de cierre es:

$\int_0^\infty x^2 j_\alpha(ux) j_\alpha(vx) dx = \frac{\pi}{2u^2} \delta(u - v)$

para α > − 1. Otra propiedad importante de la ecuación de Bessel, que se deriva de la identidad de Abel, es el Wronskiano de las soluciones:

$A_\alpha(x) \frac{dB_\alpha}{dx} - \frac{dA_\alpha}{dx} B_\alpha(x) = \frac{C_\alpha}{x},$

donde A_α y B_α son dos soluciones cualesquiera independientes de la ecuación de Bessel y C_α es una constante independiente de x (que depende de α y de las funciones de Bessel consideradas). Por ejemplo, se cumple:

$J_\alpha(x) \frac{dY_\alpha}{dx} - \frac{dJ_\alpha}{dx} Y_\alpha(x) = \frac{2}{\pi x},$

$I_\alpha(x) \frac{dK_\alpha}{dx} - \frac{dI_\alpha}{dx} K_\alpha(x) = \frac{-1}{x},$

Existe un gran número de integrales e identidades que involucran a funciones de Bessel que no están aquí reproducidas, pero que se pueden encontrar en las referencias.

Teorema del Producto

Las funciones de Bessel verifican un teorema del producto

$\lambda^{-\nu} J_{\nu}(\lambda z) = \sum_{n=0}^{\infty}\frac{1}{n!}\left(\frac{(1-\lambda^{2})z}{2}\right)^{n}J_{\nu+n}(z)$

donde λ y ν son números complejos cualesquiera. Una fórmula similar se cumple para Y_ν(z) y el resto de funciones de Bessel^{[19] [20]}

Hipótesis de Bourget

Bessel demostró que, para n no negativos, la ecuación

J_ν(x) = 0

tiene un número infinito de soluciones en x.^[21] Cuando las funciones J_n(x) se representan en la misma gráfica, ninguno de los diferentes ceros de cada función J_n(x) parece coincidir, excepto el cero situado en x = 0. Este fenómeno se conoce como Hipótesis de Bourget, en honor al matemático francés del siglo XIX que estudió las funciones de Bessel.

La hipótesis dice que, para cualesquiera enteros $n \geq 0$ and $m \geq 0$, las funciones J_n(x) y J_{n + m}(x) no tienen ceros comunes, a excepción del cero en el origen x = 0. Esta hipótesis fue demostrada por Siegel en 1929.^[22]

Derivadas de J_α, Y_α, I_α, H_α, K_α

Las siguientes fórmulas pueden encontrarse en.^[23]

Derivada bajando el índice p a p − 1

Para $y_{p}(\alpha x) = \{J_{p}(\alpha x),Y_{p}(\alpha x),I_{p}(\alpha x),H_{p}^{(1)}(\alpha x),H_{p}^{(2)}(\alpha x)\}$

$\frac{d}{dx}y_p(\alpha x)=\alpha y_{p-1}(\alpha x) - \frac{p}{x} y_p(\alpha x)$

Mientras que para y_p(αx) = K_p(αx), se tiene

$\frac{d}{dx}y_p(\alpha x)=-\alpha y_{p-1}(\alpha x) - \frac{p}{x} y_p(\alpha x)$

Derivada subiendo el índice p a p + 1 dependency

Para $y_{p}(\alpha x) = \{J_{p}(\alpha x),Y_{p}(\alpha x),K_{p}(\alpha x),H_{p}^{(1)}(\alpha x),H_{p}^{(2)}(\alpha x)\}$

$\frac{d}{dx}y_p(\alpha x)=-\alpha y_{p+1}(\alpha x) + \frac{p}{x} y_p(\alpha x)$

Mientras que para y_p(αx) = I_p(αx), se tiene

$\frac{d}{dx}y_p(\alpha x)=\alpha y_{p+1}(\alpha x) + \frac{p}{x} y_p(\alpha x)$

Otras relaciones importantes

Para $y_{p}(\alpha x) = \{J_{p}(\alpha x),Y_{p}(\alpha x),H_{p}^{(1)}(\alpha x),H_{p}^{(2)}(\alpha x)\}$, se cumplen las siguientes relaciones:

$\frac{d}{dx}y_p(\alpha x)=\frac{\alpha}{2}[y_{p-1}(\alpha x) - y_{p+1}(\alpha x)]$

$y_{p-1}(\alpha x) + y_{p+1}(\alpha x)=\frac{2p}{\alpha x}y_p(\alpha x)$

Identidades Seleccionadas

• $I_{-\frac{1}{2}} \left(\frac{z}{2}\right)+ I_{\frac{1}{2}} \left(\frac{z}{2} \right)= \frac{2 e^{\frac{z}{2}}}{\sqrt{\pi z}} ;$
• $I_\nu(z)=\sum_{k=0} \frac{z^k}{k!} J_{\nu+k}(z);$
• $J_\nu(z)=\sum_{k=0} (-1)^k \frac{z^k}{k!} I_{\nu+k}(z);$
• $I_\nu (\lambda z)= \lambda^\nu \sum_{k=0} \frac{\left((\lambda^2-1) \frac z 2 \right)^k}{k!} I_{\nu+k}(z);$
• $I_\nu (z_1+z_2)= \sum_{k=-\infty}^\infty I_{\nu-k}(z_1)I_k(z_2);$
• $J_\nu(z)=\frac z {2 \nu} (J_{\nu-1}(z)+J_{\nu+1}(z)), \quad I_\nu(z)=\frac z {2 \nu} (I_{\nu-1}(z)-I_{\nu+1}(z));$
• $J_\nu'(z)=\frac 1 2 (J_{\nu-1}(z)-J_{\nu+1}(z)), \quad I_\nu'(z)=\frac 1 2 (I_{\nu-1}(z)+I_{\nu+1}(z));$
• $\left( \frac x 2\right)^\nu= \sum_{k=0} (-1)^k \frac {\Gamma(k+\nu)}{k!} (2k+\nu) I_{2k+\nu}(x).$

Véase también

• Función de Bessel–Clifford
• Polinomios de Bessel
• Propagador
• Serie de Fourier–Bessel
• Función de Struve
• Funciones de Kelvin
• Función de Lommel
• Polinomio de Lommel

Referencias

Notas

1. ↑ Abramowitz and Stegun, p. 360, 9.1.10.
2. ↑ Abramowitz and Stegun, p. 358, 9.1.5.
3. ↑ Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.
4. ↑ Abramowitz and Stegun, p. 358, 9.1.3, 9.1.4.
5. ↑ Abramowitz and Stegun, p. 358, 9.1.6.
6. ↑ Abramowitz and Stegun, p. 360, 9.1.25.
7. ↑ Abramowitz and Stegun, p. 374, 9.6.1.
8. ↑ Abramowitz and Stegun, p. 375, 9.6.2, 9.6.10, 9.6.11.
9. ↑ Referred to as such in: Teichroew, D. The Mixture of Normal Distributions with Different Variances, The Annals of Mathematical Statistics. Vol. 28, No. 2 (Jun., 1957), pp. 510–512
10. ↑ Abramowitz and Stegun, p. 437, 10.1.1.
11. ↑ Abramowitz and Stegun, p. 438, 10.1.11, 10.1.12;
12. ↑ Abramowitz and Stegun, p. 438, 10.1.11.
13. ↑ Abramowitz and Stegun, p. 439, 10.1.39.
14. ↑ Hong Du, "Mie-scattering calculation," Applied Optics 43 (9), 1951–1956 (2004)
15. ↑ ^{a b} Arfken & Weber.
16. ↑ Abramowitz and Stegun, p. 363, 9.1.82 ff.
17. ↑ E. T. Whittaker, G. N. Watson, A course in modern Analysis p. 536
18. ↑ I.S. Gradshteyn (И.С. Градштейн), I.M. Ryzhik (И.М. Рыжик); Alan Jeffrey, Daniel Zwillinger, editors. Table of Integrals, Series, and Products, seventh edition. Academic Press, 2007. ISBN 978-0-12-373637-6. Equation 8.411.10
19. ↑ Abramowitz and Stegun, p. 363, 9.1.74.
20. ↑ C. Truesdell, "On the Addition and Multiplication Theorems for the Special Functions", Proceedings of the National Academy of Sciences, Mathematics, (1950) pp.752–757.
21. ↑ F. Bessel, Untersuchung des Theils der planetarischen Störungen, Berlin Abhandlungen (1824), article 14.
22. ↑ Watson, pp. 484–5
23. ↑ "Advanced Calculus for Engineers", F. B. Hildebrand, 6th printing, pp. 163–164 (1956)

Bibliografía

• Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 9", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 355, MR0167642, ISBN 978-0486612720, See also chapter 10.
• Arfken, George B. and Hans J. Weber, Mathematical Methods for Physicists, 6th edition (Harcourt: San Diego, 2005). ISBN 0-12-059876-0.
• Bayin, S.S. Mathematical Methods in Science and Engineering, Wiley, 2006, Chapter 6.
• Bayin, S.S., Essentials of Mathematical Methods in Science and Engineering, Wiley, 2008, Chapter 11.
• Bowman, Frank Introduction to Bessel Functions (Dover: New York, 1958). ISBN 0-486-60462-4.
• G. Mie, "Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen", Ann. Phys. Leipzig 25 (1908), p. 377.
• Olver, F. W. J.; Maximon, L. C. (2010), "Bessel function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255
• B Spain, M.G. Smith, Functions of mathematical physics, Van Nostrand Reinhold Company, London, 1970. Chapter 9 deals with Bessel functions.
• Watson, G.N., A Treatise on the Theory of Bessel Functions, Second Edition, (1995) Cambridge University Press. ISBN 0-521-48391-3.

Enlaces externos

• Lizorkin, P.I. (2001), «Bessel functions», en Hazewinkel, Michiel (en inglés), Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104 
• Karmazina, L.N.; Prudnikov, A.P. (2001), «Cylinder function», en Hazewinkel, Michiel (en inglés), Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104 
• Rozov, =N.Kh. (2001), «Bessel equation», en Hazewinkel, Michiel (en inglés), Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104 
• Wolfram function pages on Bessel J and Y functions, and modified Bessel I and K functions. Pages include formulas, function evaluators, and plotting calculators.
• Wolfram Mathworld – Bessel functions of the first kind