- Espacio de Fock
-
Espacio de Fock
El espacio de Fock
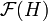 , en mecánica cuántica es un espacio de Hilbert especial, que se construye como suma directa de productos tensoriales de otro espacio de Hilbert dado
, en mecánica cuántica es un espacio de Hilbert especial, que se construye como suma directa de productos tensoriales de otro espacio de Hilbert dado 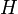 . Este espacio se usa para describir el estado cuántico de un sistema formado por un número variable o indeterminado de partículas. Recibe su nombre de Vladimir Fock.
. Este espacio se usa para describir el estado cuántico de un sistema formado por un número variable o indeterminado de partículas. Recibe su nombre de Vladimir Fock.Contenido
Definición
Técnicamente, el espacio de Fock es el espacio de Hilbert preparado como suma directa de los productos tensoriales de los espacios de Hilbert para una partícula:
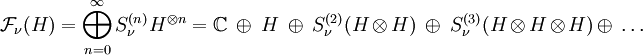
donde Sν es el operador que simetriza (o antisimetriza) el espacio, de forma que el espacio de Fock describa adecuadamente a un conjunto de bosones ν=+ (o fermiones ν=-). H es el espacio de Hilbert para una sola partícula. Esta forma de combinación de H, que resulta en un espacio de Hilbert "mayor" (el espacio de Fock), contiene estados para un número arbitrario de partículas.[1]
Los estados de Fock son la base natural para este espacio.
Espacio de Fock bosónico
Esta construcción se realiza usando como proyector uno que simetriza los elementos, por ejemplo, para simetrizar el producto de dos vectores que representan cada el estado de una partícula:
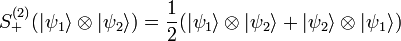
Este último estado simetrizado representa un estado con dos bosones indistinguibles. Para el caso de n vectores el operador de simetrización viene dado por:
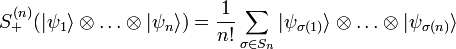
Donde el sumatorio se extiende a todas las permutaciones posibles del grupo simétrico de orden n. Obviamente la simetrización de los espacios de cero y de una partícula son triviales:
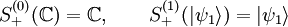
Espacio de Fock fermiónico
Generalizando los resultados de la sección anterior construimos los operadores de antisimetrización. El antisimetrizador de dos partículas viene dado por:
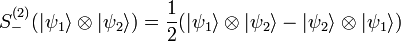
Así este estado antisimetrizado representa, por tanto, un estado con dos fermiones indistinguibles. Para el caso de n fermiones un estado vendría dado por:
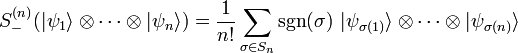
Donde nuevamente el sumatorio se extiende a todas las permutaciones posibles del grupo simétrico de orden n y donde
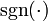 es el signo de la permutación (+1 si es par, -1 si es impar).
es el signo de la permutación (+1 si es par, -1 si es impar).Referencia
- ↑ Téngase en cuenta de que aunque el espacio es aparene mayor, el espacio de Fock es un espacio de Hilbert separable y por tanto puede construirse un isomorfismo con el espacio original al ser también separable, por lo que la construcción de Fock puede considerarse más bien una manera de representar el espacio de Fock más que un ente matemáticamente diferente.
Bibliografía
- H. Halvorson & M. Müger (2006) Chapter IV, "Algebraic Quantum Field Theory".
Véase también
Categoría: Mecánica cuántica
Wikimedia foundation. 2010.
