- Ecuación de Klein-Gordon
-
Ecuación de Klein-Gordon
La ecuación de Klein-Gordon o ecuación K-G debe su nombre a Oskar Klein y Walter Gordon, y es la ecuación que describe un campo escalar libre en teoría cuántica de campos.
Contenido
Historia
La ecuación de Klein-Gordon fue propuesta originalmente por Erwin Schrödinger como ecuación para la función de onda de una partícula cuántica. Sin embargo, puesto que la ecuación de Klein-Gordon no admitía una interpretación probabilista adecuada entre otros problemas, Schrödinger consideró más adecuado pasar a una versión no relativista de la ecuación que es la que actualmente se conoce como ecuación de Schrödinger.
Más tarde la función de onda que aparece en la ecuación de Klein-Gordon sería apropiadamente interpretada como la densidad de un campo bosónico cargado de espín cero. Así el hecho de que la "densidad de probabilidad" fuera negativa era interpretada como una densidad de carga negativa y los problemas de interpretación como probabilidades de presencia desaparecían, aunque persistían otros de los problemas mencionados más adelante. Sin embargo, dentro de la teoría cuántica de campos la ecuación de Klein-Gordon sí resultó útil.
Forma de la ecuación
La ecuación de Klein-Gordon para partículas en un espacio-tiempo plano tiene la siguiente forma:
(1)
![\left [\frac{1}{c^2}\frac{\partial^2}{\partial t^2} - \nabla^2 + \frac{m^2c^2}{\hbar^2} \right ] \phi = 0](/pictures/eswiki/102/f123ca6f668cc2b58529bb50c8e1c806.png)
Usando el operador D'Alambertiano
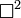 y el parámetro de masa
y el parámetro de masa 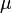 definidos como:
definidos como: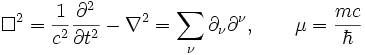
La ecuación puede escribirse se escribe de manera más compacta y manifiestamente covariante:
(2)
![\left [\Box ^2 + \mu^2 \right ] \phi = 0](/pictures/eswiki/100/d5f71120d633258f498eb9d631f2015b.png)
Nótese que si se escoge la métrica con signatura opuesta, aparece un signo menos delante de
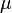 en esta última ecuación.
en esta última ecuación.En un espacio-tiempo general la ecuación de Klein-Gordon puede escribirse como:
(3)
![\left [\frac{1}{\sqrt{-g}}\frac{\part}{\part x^\alpha}\left(\sqrt{-g}\ g^{\alpha\beta} \frac{\part \phi}{\part x^\beta} \right) \right]+ \frac{m^2c^2}{\hbar^2}\phi = 0](/pictures/eswiki/97/a79886476449363e0f7b7c80cf83ac8a.png)
Donde:
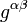 , son las componentes contravariantes del tensor métrico.
, son las componentes contravariantes del tensor métrico.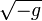 , es la raíz cuadrada del determinante cambiado de signo.
, es la raíz cuadrada del determinante cambiado de signo.
La ecuación K-G en mecánica cuántica
Inicialmente la ecuación KG se introdujo en mecánica cuántica con la pretensión de modelizar la ecuación de movimiento para una partícula cuántica y relativista. De este modo, se deduce la ecuación escribiendo la energía que tiene una partícula relativista y utilizando la forma de los operadores Hamiltoniano y momento en mecánica cuántica:
![E^2 = \mathbf{p}^2 c^2 + m^2 c^4= \left [i \hbar \frac{\partial}{\partial t} \right ] ^2
\quad \quad , \quad \mathbf{p}=-i\hbar \nabla](/pictures/eswiki/98/b2c692b6e6285bce6e4746c33c213745.png)
Existe varios problemas si tratamos de interpretar la variable dinámica
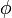 como una función de onda, ya que aparecen varias incongruencias como:
como una función de onda, ya que aparecen varias incongruencias como:- El que la energía no esté acotada inferiormente, lo que daría lugar a partículas inestables. Este problema de interpretación que también lo presentaba la ecuación de Dirac, hasta que se presentó la interpretación de las energías negativas como antipartículas.
- La densidad de probabilidad asociada a esta función de onda no es definida positiva, por lo que el cuadrado de la módulo del campo de Klein-Gordon, a diferencia de lo que sucede con una función de onda ordinaria no puede ser interpretado como una probabilidad. La "densidad" conservada en la evolución temporal es:
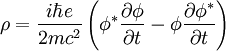
- Que puede ser negativa, por lo que no admitía una interpretación en términos de probabilidades positivas. Esa última fue la razón del abandono de la ecuación de Klein-Gordon como ecuación viable dentro de la mecánica cuántica para describir partículas cuánticas relativistas.
- Aunque la ecuación de Klein-Gordon precide correctamente el desdoblamiento observado de los niveles energéticos de los átomos hidrogenoides 2s y 2p, lográndose un mejor acuerdo cualitativo el acuerdo cuantitativo no es bueno. El cálculo mediante la ecuación de Klein-Gordon predice que los niveles energéticos
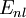 del átomo hidrogenoide son:
del átomo hidrogenoide son:
![E_{nl} = -\frac{R\hbar Z^2}{n^2} \left[1+
\frac{\alpha^2Z^2}{n^2} \left(\frac{n}{l+\frac{1}{2}} -\frac{3}{4} \right)+ \dots \right]](/pictures/eswiki/102/f4e75707b1bb98f5ee2c390148ac8937.png)
- El primer término de la expresión anterior coincde con el predicho por la ecuación de Schrödinger, pero el segundo es unas tres veces más grandes que el valor observado, y correctamente predicho por la ecuación de Dirac.
- Finalmente, la ecuación de Klein-Gordon tampoco tiene en cuenta adecuadamente el spin de ciertas partículas, por lo que no podía representar adecuadamente partículas como los electrones que tienen espín 1/2.
La ecuación K-G en teoría cuántica de campos
En teoría cuántica de campos el objeto fundamental no es la función de onda sino el propio estado físico del vacío o espacio-tiempo. Los campos físicos y las partículas materiales se conciben en este enfoque como operadores autoadjuntos definidos sobre el conjunto de estados del espacio-tiempo. La presencia de campo en una determinada región del espacio-tiempo comporta que el existe un operador autoadjunto asociado campo de esa región. En ese nuevo enfoque la variable el operador cuántico asociado a la variable
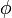 es un campo, que no necesita dar lugar a una densidad de probabilidad positiva. De hecho en el formalismo de la mecánica cuántica de campos el campo de Klein-Gordon describe un tipo de campo que tratado mediante la cuantización canónica describe un campo escalar con carga eléctrica de spin 0 (bosón), por ejemplo, los mesones π pueden ser descritos mediante la ecuación K-G. Para describir campos de spin 1/2 se utiliza la ecuación de Dirac.
es un campo, que no necesita dar lugar a una densidad de probabilidad positiva. De hecho en el formalismo de la mecánica cuántica de campos el campo de Klein-Gordon describe un tipo de campo que tratado mediante la cuantización canónica describe un campo escalar con carga eléctrica de spin 0 (bosón), por ejemplo, los mesones π pueden ser descritos mediante la ecuación K-G. Para describir campos de spin 1/2 se utiliza la ecuación de Dirac.La descripción de un campo en teoría cuántica de campos parte de una cierta densidad lagrangiana que a partir del principio de mínima acción proporciona la ecuación de movimento que define su evolución temporal. La densidad de Lagrangiano de la que se deriva la ecuación de Klein-Gordon variando la acción o mediante las ecuaciones de Euler-Lagrange es
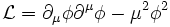
Donde el campo es real. En este caso la partícula que surje como excitación de este campo no tiene carga y su antipartícula es ella misma. Para describir una partícula escalar con carga, y a su antipartícula, la densidad lagrangiana se toma como:
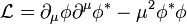
Se obtiene entonces una ecuación de Klein-Gordon para
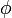 y otra para su complejo conjugado
y otra para su complejo conjugado 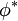 .
.Solución general
Se puede hacer un desarrollo en ondas planas y la solución general para un campo real de Klein-Gordon es entonces
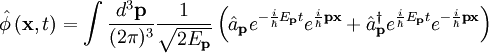
Estando relacionada la energía con la masa y el trimomento mediante la relación de dispersión
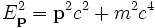
Donde
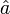 y
y 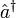 son los coeficientes del desarrollo, y una vez efectuada la segunda cuantización se convierten en operadores de creación y destrucción de las partículas bosónicas del campo, que de hecho son formalmene simliares a los operadores creación y destrucción que intervienen en el oscilador armónico cuántico. Es entonces cuando se pone de manifiesto el carácter bosónico de la ecuación de Klein-Gordon, y se puede hacer la interpretación del campo
son los coeficientes del desarrollo, y una vez efectuada la segunda cuantización se convierten en operadores de creación y destrucción de las partículas bosónicas del campo, que de hecho son formalmene simliares a los operadores creación y destrucción que intervienen en el oscilador armónico cuántico. Es entonces cuando se pone de manifiesto el carácter bosónico de la ecuación de Klein-Gordon, y se puede hacer la interpretación del campo 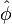 como un conjunto de infinitos osciladores armónicos cuánticos desacoplados.Categorías: Ecuaciones | Mecánica cuántica | Teoría cuántica de campos
como un conjunto de infinitos osciladores armónicos cuánticos desacoplados.Categorías: Ecuaciones | Mecánica cuántica | Teoría cuántica de campos
Wikimedia foundation. 2010.
