- Diffie-Hellman
-
Diffie-Hellman
El protocolo Diffie-Hellman[1] (debido a Whitfield Diffie y Martin Hellman) permite el intercambio secreto de claves entre dos partes que no han tenido contacto previo, utilizando un canal inseguro, y de manera anónima (no autenticada).
Se emplea generalmente como medio para acordar claves simétricas que serán empleadas para el cifrado de una sesión.
Siendo no autenticado, sin embargo provee las bases para varios protocolos autenticados.
Su seguridad radica en la extrema dificultad (conjeturada, no demostrada) de calcular logaritmos discretos en un campo finito.
Contenido
Versión básica
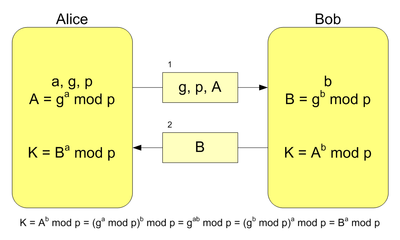
Para dos partes A y B que intentan establecer una clave secreta y un adversario E, la versión básica es como sigue:
- Se establecen un primo p y un generador
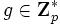 ([2] ). Estos son públicos, conocidos no sólo por las partes A y B sino también por el adversario E.
([2] ). Estos son públicos, conocidos no sólo por las partes A y B sino también por el adversario E. - A escoge
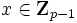 al azar, calcula X = gxmod p, y envía X a B
al azar, calcula X = gxmod p, y envía X a B - B escoge
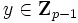 al azar, calcula Y = gymod p, y envía Y a A
al azar, calcula Y = gymod p, y envía Y a A
Nótese que Xy = (gx)y = gxy = (gy)x = Yx, con todas las operaciones en el grupo
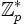 . Llamemos K a esta cantidad común: el hecho destacable es que ambas partes pueden calcularla, y por lo tanto obtener una clave compartida.
. Llamemos K a esta cantidad común: el hecho destacable es que ambas partes pueden calcularla, y por lo tanto obtener una clave compartida.Un adversario E que poseyera p, g, X e Y, podría calcular el secreto compartido si tuviera también uno de los valores privados (x o y) o lograse invertir la función. Pero calcular x dado X es el problema del logaritmo discreto en
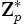 , un problema que se cree intratable computacionalmente. El mismo protocolo, y otros basados en este, pueden llevarse a cabo en cualquier grupo en que a la vez la exponenciación sea simple y el logaritmo discreto difícil, como el grupo multiplicativo análogo de los campos de Galois
, un problema que se cree intratable computacionalmente. El mismo protocolo, y otros basados en este, pueden llevarse a cabo en cualquier grupo en que a la vez la exponenciación sea simple y el logaritmo discreto difícil, como el grupo multiplicativo análogo de los campos de Galois 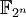 o el grupo de puntos definidos por una curva elíptica sobre un campo finito.
o el grupo de puntos definidos por una curva elíptica sobre un campo finito.Sin embargo, el protocolo es sensible a ataques activos del tipo "hombre en el medio" (mitm, man-in-the-middle). Si la comunicación es interceptada por un tercero, éste se puede hacer pasar por el emisor cara al destinatario y viceversa, ya que no se dispone de ningún mecanismo para validar la identidad de los participantes en la comunicación. Así, el "hombre en el medio" podría acordar una clave con cada participante y retransmitir los datos entre ellos, escuchando la conversación en ambos sentidos.
Ejemplo del protocolo
A Sec Calc p, g a ga mod p … (gb mod p)a mod p 
= B Calc Sec p, g b … gb mod p (ga mod p)b mod p - A y B acuerdan usar el número primo p=23 y la base g=5.
- A elige un número secreto a=6, luego envía a B (ga mod p)
- 56 mod 23 = 8.
- B elige un número secreto b=15, luego envía a A (gb mod p)
- 515 mod 23 = 19.
- A calcula (gb mod p)a mod p
- 196 mod 23 = 2.
- B calcula (ga mod p)b mod p
- 815 mod 23 = 2.
Valores mucho más grandes de a,b y p se necesitarían para hacer este ejemplo seguro. Dado que es muy sencillo probar todos los valores posibles de gab mod 23 (habrá, como máximo, 22 valores, inclusive si a y b son números grandes). Si p fuera un primo de más de 300 dígitos, y a y b fueran por lo menos de 100 dígitos, entonces hasta el mejor algoritmo para encontrar a dado g, p, y ga mod p tomaría más tiempo que la vida del universo para resolverse. g no necesita ser grande, y en la práctica es usualmente 2 o 5.
Versiones más complejas
- El protocolo ElGamal de negociación de claves[3] provee negociación en un solo paso y autenticación unilateral (del receptor hacia el emisor) si la clave pública del receptor es conocida de antemano por el emisor.
- El protocolo MTI/A0,[4] empleando dos mensajes y sin requerir firmas, proporciona claves de sesión variables en el tiempo con mutua autenticación implícita de claves contra ataques pasivos.
- El protocolo STS[5] es una variante de tres pasos de la versión básica que permite el establecimiento de una clave secreta compartida entre dos partes con mutua autenticación de entidades y mutua autenticación explícita de las claves. El protocolo también facilita el anonimato: las identidades de A y B pueden protegerse contra el adversario E. El método emplea firmas digitales.
Referencias
- ↑ Diffie, W. y M.E.Hellman. "New directions in cryptography", IEEE Transactions on Information Theory 22 (1976), pp. 644-654.
- ↑ Aquí
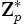 es el conjunto de los enteros menores que p que son primos relativos de p, que es un grupo bajo la multiplicación módulo p.
es el conjunto de los enteros menores que p que son primos relativos de p, que es un grupo bajo la multiplicación módulo p. - ↑ El Gamal, T. Cryptography and logarithms over finite fields, tesis de PhD, Stanford University, 1984.
- ↑ Matsumoto, T., Y. Takashima y H. Imai. "On seeking smart public-key distribution systems", The Transactions of the IECE of Japan E69 (1986), pp. 99-106
- ↑ Diffie, W., P.C. van Oorschot y M.J. Wiener. "Authentication and authenticated key exchanges", Design, Codes and Cryptography 2 (1992), pp. 107-125.
Bibliografía adicional
- Menezes, A.J., P.C. van Oorschot y S.A. Vanstone. Handbook of Applied Cryptography. Boca Raton, Fl.: CRC Press, 1997.
Categoría: Criptografía - Se establecen un primo p y un generador
Wikimedia foundation. 2010.