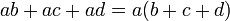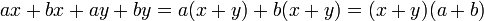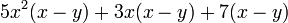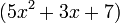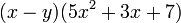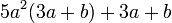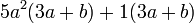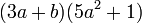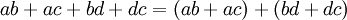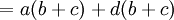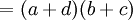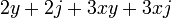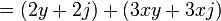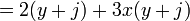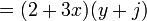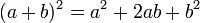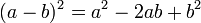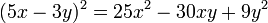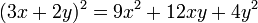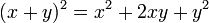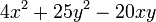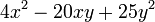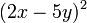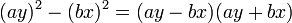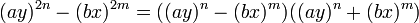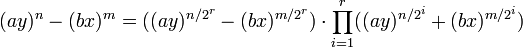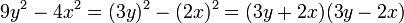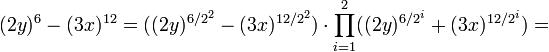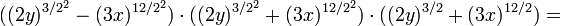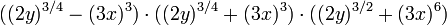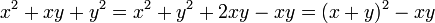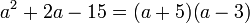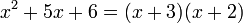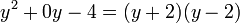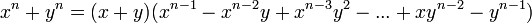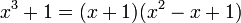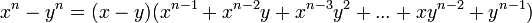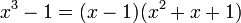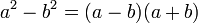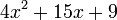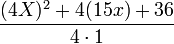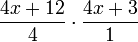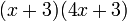Factorización

Factorización

Saltar a navegación, búsqueda

En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos utilizar los números primos) que, al multiplicarlos todos, resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y a²-b² se factoriza como binomio conjugados (a - b)(a + b).

La factorización de enteros en números primos se describe en el teorema fundamental de la aritmética y la factorización de polinomios (en ciertos contextos) en el teorema fundamental del álgebra.

Factorizar un polinomio

Antes que nada, hay que decir que no todo polinomio se puede factorizar utilizando números reales, si se consideran los números complejos sí se puede. Existen métodos de factorización, para algunos casos especiales.

• Binomios

1. Diferencia de cuadrados
2. Suma o diferencia de cubos
3. Suma o diferencia de potencias impares iguales

• Trinomios

1. Trinomio cuadrado perfecto
2. Trinomio de la forma x²+bx+c
3. Trinomio de la forma ax²+bx+c

• Polinomios

1. Factor común

Caso I - Factor común

Sacar el factor común es extraer la literal común de un polinomio, binomio o trinomio, con el menor exponente y el divisor común de sus coeficientes.

Factor común monomio

Factor común por agrupación de términos

$ab + ac + ad = a ( b + c + d) \,$

$ax + bx + ay + by = a (x+y) + b (x+y) = (x+y)(a + b ) \,$

Factor común polinomio

Primero hay que determinar el factor común de los coeficientes junto con el de las variables (la que tenga menor exponente). Se toma en cuenta aquí que el factor común no solo cuenta con un término, sino con dos.

un ejemplo:

$5x^2(x-y) + 3x(x-y) +7(x-y) \,$

Se aprecia claramente que se esta repitiendo el polinomio (x-y), entonces ese será el factor común. El otro factor será simplemente lo que queda del polinomio original, es decir:

$(5x^2 + 3x +7) \,$

La respuesta es:

$(x -y)(5x^2 + 3x +7) \,$

En algunos casos se debe utilizar el número 1, por ejemplo:

$5a^2(3a+b) +3a +b \,$

Se puede utilizar como:

$5a^2(3a+b) + 1(3a+b) \,$

Entonces la respuesta es:

$(3a+b) (5a^2+1) \,$

Caso II - Factor común por agrupación de términos

Para trabajar un polinomio por agrupación de términos, se debe tener en cuenta que son dos características las que se repiten. Se identifica porque es un número par de términos. Para resolverlo, se agrupan cada una de las características, y se le aplica el primer caso, es decir:

$ab+ac+bd+dc = (ab+ac)+(bd+dc)\,$

$= a(b+c)+d(b+c)\,$

$= (a+d) (b+c)\,$

Un ejemplo numerico puede ser:

$2y + 2j +3xy + 3xj\,$

entonces puedes agruparlos de la siguiente manera:

$= (2y+2j)+(3xy+3xj)\,$

Aplicamos el primer caso (Factor común)

$= 2(y+j)+3x(y+j)\,$

$= (2+3x)(y+j)\,$

Caso III - Trinomio cuadrado perfecto

Se identifica por tener tres términos, de los cuales dos tienen raíces cuadradas exactas, y el restante equivale al doble producto de las raíces del primero por el segundo. Para solucionar un T.C.P. debemos reordenar los términos dejando de primero y de tercero los términos que tengan raíz cuadrada, luego extraemos la raíz cuadrada del primer y tercer término y los escribimos en un paréntesis, separándolos por el signo que acompaña al segundo término, al cerrar el paréntesis elevamos todo el binomio al cuadrado.

$(a+b)^2 = a^2+2ab+b^2\,$

y

$(a-b)^2 = a^2-2ab+b^2\,$

Ejemplo 1:

$(5x-3y)^2 = 25x^2-30xy+9y^2\,$

Ejemplo 2:

$(3x+2y)^2 = 9x^2+12xy+4y^2\,$

Ejemplo 3:

$(x+y)^2 = x^2+2xy+y^2\,$

Ejemplo 4:

$4x^2+25y^2-20xy\,$

Organizando los términos tenemos

$4x^2 - 20xy + 25y^2\,$

Extrayendo la raíz cuadrada del primer y último término y agrupándolos en un paréntesis separados por el signo del segundo término y elevando al cuadrado nos queda:

$(2x - 5y)^2\,$

Al verificar que el doble producto del primero por el segundo termino es -20xy determinamos que es correcta la solución. De no ser así, esta solución no aplicaría.

Caso IV - Diferencia de cuadrados

Se identifica por tener dos términos elevados al cuadrado y unidos por el signo menos. Se resuelve por medio de dos paréntesis, (parecido a los productos de la forma (a-b)(a+b), uno negativo y otro positivo.

$(ay)^2-(bx)^2= (ay-bx)(ay+bx)\,$

O en una forma mas general para exponentes pares:

$(ay)^{2n}-(bx)^{2m}= ((ay)^n-(bx)^m)((ay)^n+(bx)^m)\,$

Y utilizando una productoria podemos definir una factorizacion para cualquier exponente, el resultado nos da r+1 factores.

$(ay)^n-(bx)^m= ((ay)^{n/{2^r}}-(bx)^{m/{2^r}})\cdot \prod_{i=1}^{r} ((ay)^{n/{2^i}}+(bx)^{m/{2^i}}) \,$

Ejemplo 1:

$9y^2-4x^2= (3y)^2-(2x)^2= (3y+2x)(3y-2x)\,$

Ejemplo 2: Supongamos cualquier r, r=2 para este ejemplo.

$(2y)^6-(3x)^{12}= ((2y)^{6/2^2}-(3x)^{12/2^2})\cdot\prod_{i=1}^{2} ((2y)^{6/{2^i}}+(3x)^{12/{2^i}})= \,$

$((2y)^{3/2^2}-(3x)^{12/2^2})\cdot((2y)^{3/2^2}+(3x)^{12/2^2})\cdot((2y)^{3/2}+(3x)^{12/2})= \,$

$((2y)^{3/4}-(3x)^{3})\cdot((2y)^{3/4}+(3x)^{3})\cdot((2y)^{3/2}+(3x)^{6}) \,$

La factorización de la diferencia o resta de cuadrados consiste en obtener las raíz cuadrada de cada término y representar estas como el producto de binomios conjugados.

Caso V - Trinomio cuadrado perfecto por adición y sustracción

Se identifica por tener tres términos, dos de ellos son cuadrados perfectos, pero el restante hay que completarlo mediante la suma para que sea el doble producto de sus raíces, el valor que se suma es el mismo que se resta para que el ejercicio original no cambie.

$x^2+xy+y^2=x^2+y^2+2xy-xy=(x+y)^2-xy\,$

Caso VI - Trinomio de la forma x² + bx + c

Se identifica por tener tres términos, hay una literal con exponente al cuadrado y uno de ellos es el término independiente. Se resuelve por medio de dos paréntesis, en los cuales se colocan la raíz cuadrada de la variable, buscando dos números que multiplicados den como resultado el término independiente y sumados (pudiendo ser números negativos) den como resultado el término del medio.

Ejemplo:

$a^2+2a-15 = (a+5) (a-3) \,$

Ejemplo:

$x^2+5x+6 = (x+3)(x+2)\,$

Ejemplo:

$y^2+0y-4 = (y+2)(y-2)\,$

Caso VII Suma o diferencia de potencias a la n

La suma de dos números a la potencia n, aⁿ +bⁿ se descompone en dos factores (siempre que n sea un número impar):

Quedando de la siguiente manera:

$x^n + y^n = (x+y)(x^{n-1}-x^{n-2}y+x^{n-3}y^2-... + xy^{n-2}-y^{n-1}) \,$

Ejemplo:

$x^3+1 = (x+1)(x^2-x+1) \,$

La diferencia también es factorizable y en este caso no importa si n es par o impar. Que dando de la siguiente manera:

$x^n-y^n = (x-y)(x^{n-1}+x^{n-2}y+x^{n-3}y^2 +... +xy^{n-2}+y^{n-1}) \,$

Ejemplo:

$x^3-1 = (x-1)(x^2+x+1) \,$

$a^2-b^2 = (a-b)(a+b) \,$

Las diferencias, ya sea de cuadrados o de cubos salen de un caso particular de esta generalización.

Caso VIII Trinomio de la forma ax² + bx + c

En este caso se tienen 3 términos: El primer término es un cuadrado perfecto, osea que tiene raíz cuadrada exacta, el segundo término tiene la mitad del exponente del término anterior y el tercer término es un término independiente, osea sin una parte literal, así:

$4x^2+15x+9\,$

Para factorizar una expresion de esta forma; primero se coje el término al lado de x², (en este caso el 4) y se multiplica por toda la expresión, dejando el segundo término igual pero en parentesis y dejando todo esto en una fracción. Usando como denominador el término que estamos multiplicando, multiplicandolo con el 1

$\frac{(4X)^2+4(15x)+36}{4\cdot 1}\,$

Luego separamos en dos fracciones el término

$\frac{4x+12}{4}\cdot \frac{4x+3}{1}\,$

Y después procedemos a eliminar las fracciones

$(x+3)(4x+3)\,$

CASO 9 CUBO PERFECTO DE BINOMIOS

teniendo en cuenta que los productos notables nos dicen que: (a+b)3 = a^3+3a^2b+3ab^2+b^3 y (a-b)^3-3a^2b+3ab^2-b^3

Obtenido de "Factorizaci%C3%B3n"