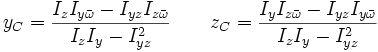- Centro de cortante
-
Centro de cortante
En resistencia de materiales, el centro de cortante (también llamado centro de torsión, centro de cortadura o centro de esfuerzos cortantes (CEC)), es un punto situado en el plano de la sección transversal de una pieza prismática como una viga o un pilar tal que cualquier esfuerzo cortante que pase por él no producirá momento torsor en la sección transversal de la pieza, esto es, que todo esfuerzo cortante genera un momento torsor dado por la distancia del esfuerzo cortante al centro de cortante. Se suele denotar por (yC, zC).
Cuando existe un eje de simetría el centro de cortante está situado sobre él. En piezas con dos ejes de simetría el centro de cortante coincide con el centro de gravedad de la sección y en ese caso la flexión y torsión están desacopladas y una viga o pilar puede tener flexión sin torsión y torsión sin flexión. Sin embargo, en prismas mecánicos, vigas o pilares con asimetrías en su sección transversal es necesario determinar el centro de cortante para determinar correctamente las tensiones.
Definición del centro de cortante
Si usamos la coordenada x para medir distancias a lo largo del eje de una pieza prismática y las coordenadas (y, z) para las coordenadas de cualquier punto sobre una sección transversal. El centro de cortantes es el punto definido por las coordenadas (yC, zC) dadas por:
Donde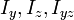 son los momentos de área y el producto de inercia. Y donde
son los momentos de área y el producto de inercia. Y donde 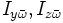 son los productos de inercia sectoriales definidos como:
son los productos de inercia sectoriales definidos como:
Y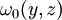 es la función auxiliar del alabeo unitario.
es la función auxiliar del alabeo unitario.Es importante señalar que:
- Si el eje Y es un eje de simetría de la sección transversal entonces zC = zG.
- Si el eje Z es un eje de simetría de la sección transversal entonces yC = yG.
- Si una pieza tiene dos ejes de simetría Y y Z (como sucede secciones circulares, rectangulares, elípticas, romboidales, secciones en I y secciones en H, entre otras) y se consideran coordendas baricéntricas entonces yC = yG = 0 y zC = zG = 0,.
Coincidencia del centro de cortantes y el polo de torsión
Cuando un prisma mecánico, viga o pilar con asimetrías en su sección transversal se somete a flexión aparece torsión girando toda la sección alrededor de un cierto punto llamado polo de torsión. Puede demostrarse que el polo de torsión y el centro de cortantes coinciden.
Ejemplos
Categoría: Resistencia de materiales
Wikimedia foundation. 2010.